Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Kräfte als Vektoren

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Kräfte lassen sich durch Vektoren beschreiben. Die Richtung der Kraft entspricht der Richtung des Vektors und ihre Größe der Länge des Vektors. Angriffspunkt der Kraft ist der Anfangspunkt der gerichteten Strecke, die den Vektor repräsentiert.

Verschiedene Kräfte superponieren sich, die resultierende Kraft entspricht genau der Summe der Vektoren, wenn die Vektoraddition komponentenweise definiert wird, d.h. ist $ x = (x_1, \ldots , x_n), y = (y_1, \ldots y_n)$ dann ist

$\displaystyle x + y := (x_1 + y_1, \ldots , x_n + y_n) .$

Geometrisch wird dies durch das sogenannte Kräfteparallelogramm veranschaulicht.

Beispiel: Am Punkt $ (1,1,0)$ greifen die Kräfte $ \vec{K}_1 = (2,0,1)$, $ \vec{K}_2 = (0,1,1)$ und $ \vec{K}_3 = (-2,-1,1)$ an.

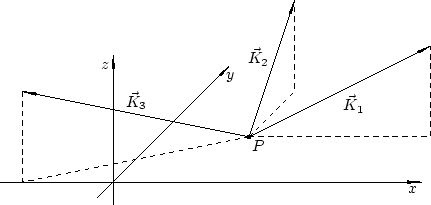
\includegraphics{kraefte.eps}

Die resultierende Kraft ergibt sich durch Vektoraddition:

$\displaystyle (2,0,1) + (0,1,1) + (-2,-1,1) = (0,0,3) $

Der Betrag etwa der Kraft $ \vec{K}_1$ ist

$\displaystyle \vert\vec{K}_1\vert = \sqrt{2^2 + 0^2 + 1^2} = \sqrt{5} $

Ist $ \lambda \in \mathbb{R}$ und $ x = (x_1, \ldots , x_n) \in {\mathbb{R}^n} $ gegeben, dann definiert man eine Skalarmultiplikation durch

$\displaystyle \lambda \cdot x := (\lambda x_1, \ldots , \lambda x_n) .$

Anschaulich bedeutet die Skalarmultiplikation mit $ \lambda $ , daß der Vektor $ x$ um den Faktor $ \lambda $ gestreckt wird bzw. die durch $ x$ repräsentierte Kraft um den Faktor $ \lambda $ verändert wird. Man beachte, daß sich bei negativem $ \lambda $ die Richtung des Vektors (bzw. der Kraft) umkehrt.

(Aus: Lineare Algebra und Geometrie, Kimmerle)
[Verweise]
  automatisch erstellt am 25.  1. 2006