Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Singuläres wirbelfreies Feld

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht
Wir betrachten das ebene Vektorfeld

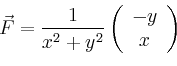
\begin{displaymath} \vec{F}=\frac{1}{x^2+y^2}\left( \begin{array}{c} -y\\ x\\ \end{array}\right) \end{displaymath}

auf der Kreisscheibe

$\displaystyle K:\quad x^2+y^2\leq r\,,\quad r>0\,. $

Obwohl die Rotation von $ \vec{F}$ verschwindet,

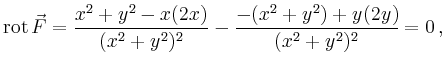
$\displaystyle \operatorname{rot}\vec{F} = \frac{x^2+y^2-x(2x)}{(x^2+y^2)^2} -\frac{-(x^2+y^2)+y(2y)}{(x^2+y^2)^2} = 0\,, $

ist das Arbeitsintegral über den Rand $ C$ von $ K$ nicht null. Verwendet man

\begin{displaymath} \vec{r}(t)=r\left( \begin{array}{c} \cos t\\ \sin t\\ \end{array}\right),\quad t\in[0,2\pi]\,, \end{displaymath}

als Parametrisierung für $ C$, so erhält man

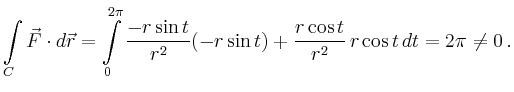
$\displaystyle \int\limits_{C} \vec{F} \cdot d\vec{r} = \int\limits_0^{2\pi} \frac{-r\sin t }{r^2}(-r\sin t )+\frac{r\cos t}{r^2}\,r\cos t\, dt = 2\pi \neq 0\,. $

Dies ist kein Widerspruch zum Satz von Green, weil das Vektorfeld $ \vec{F}$ im Inneren der Kreisscheibe bei $ (0,0)$ eine Singularität besitzt.

[Verweise]
  automatisch erstellt am 9. 10. 2013