Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Beispiel: Fluss durch einen Funktionsgraph

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht
Es soll der Fluss des Vektorfeldes

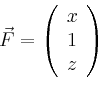
\begin{displaymath} \vec{F}=\left( \begin{array}{c} x\\ 1\\ z\\ \end{array}\right) \end{displaymath}

nach oben durch den Graph der Funktion

$\displaystyle z=f(x,y)=x^2-y $

über dem Bereich

$\displaystyle D:\quad\vert x\vert+\vert y\vert\leq 1 $

berechnet werden.

Da sowohl das Vektorfeld als auch der Funktionsgraph symmetrisch zur $ yz$-Ebene sind, genügt es, den Bereich $ D$ für $ x\geq 0$ zu betrachten und das Ergebnis zu verdoppeln. Für den Gesamtfluss erhält man damit

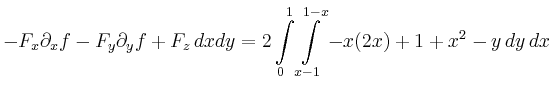$\displaystyle \iint\limits_D$ $\displaystyle -F_x\partial_x f-F_y \partial_y f+F_z\,dxdy = 2\int\limits_{0}^1\int\limits_{x-1}^{1-x}-x(2x)+1+x^2-y\,dy\,dx$    
  $\displaystyle =2\int\limits_{0}^1 \left[-x^2y+y-\frac{1}{2}y^2\right]_{y=x-1}^{y=1-x}\,dx = \int\limits_{0}^1 4x^3-4x^2-4x+4\,dx$    
  $\displaystyle = \left[x^4-\frac{4}{3}x^3-2x^2+4x\right]_{0}^1 = \frac{5}{3}\,.$    

[Verweise]
  automatisch erstellt am 2. 10. 2013