Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon: Erläuterung zu

Reelle Zahlen

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht
Die Menge $ \mathbb{R}$ aller (endlichen und unendlichen) Dezimalzahlen bezeichnet man als reelle Zahlen. Die reellen Zahlen können mit den Punkten auf der Zahlengeraden identifiziert werden. Eine Zahl $ x$ entspricht dem Abstand von Nullpunkt, wobei das Vorzeichen angibt, ob $ x$ zur positiven oder negativen Halbachse gehört.

\includegraphics[width=.5\linewidth]{a_reelle_zahlen_bild}

Die rationalen Zahlen $ \mathbb{Q}$ liegen dicht in $ \mathbb{R}$, d.h. jede irrationale Zahl $ x\in \mathbb{R}\backslash \mathbb{Q}$ läßt sich beliebig genau durch Brüche approximieren. Im Gegensatz zu $ \mathbb{Q}$ ist $ \mathbb{R}$ jedoch nicht abzählbar.

Die reellen Zahlen bilden mit der Addition und Multiplikation einen Körper. Darüberhinaus sind sie vollständig, d.h. jede konvergente Folge reeller Zahlen besitzt einen Grenzwert in $ \mathbb{R}$.

Mit dem auf Georg Cantor zurückgehenden sogenannten Cantorschen Diagonalverfahren kann gezeigt werden, dass $ \mathbb{R}$ nicht abzählbar ist.

Die Beweisführung ist inderekt.
Es wird angenommen, dass $ \mathbb{R}$ abzählbar ist. Dann können alle Zahlen zwischen 0 und $ 1$ in eine Reihenfolge gebracht werden. Schreibt man diese Zahlen nun als nicht abbrechende Dezimalbrüche


$\displaystyle 1$ $\displaystyle :$ $\displaystyle 0.a_{1,1}a_{1,2}a_{1,3}a_{1,4}...$  
$\displaystyle 2$ $\displaystyle :$ $\displaystyle 0.a_{2,1}a_{2,2}a_{2,3}a_{2,4}...$  
$\displaystyle 3$ $\displaystyle :$ $\displaystyle 0.a_{3,1}a_{3,2}a_{3,3}a_{3,4}...$  
$\displaystyle \vdots$ $\displaystyle :$ $\displaystyle \vdots$  

so kann durch die Vorschrift

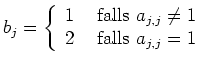
$\displaystyle b_j = \left\{\begin{array}{rl}1 & \textrm{ falls } a_{j,j} \neq 1\\ 2 & \textrm{ falls } a_{j,j} = 1 \end{array}\right. $

eine Zahl $ b=0.b_1b_2b_3... $ konstruiert werden, die auch zwischen 0 und $ 1$ liegt, sich aber an der $ j$-ten Stelle von der $ j$-ten Zahl der Abzählung unterscheidet, also nicht in der Liste auftritt. Dies ist aber ein Widerspruch zu der Annahme, dass in der Liste alle Zahlen vorkommen und daher ist $ \mathbb{R}$ nicht abzählbar.

(Autor: J. Hörner)
[Zurück zur Aussage]
  automatisch erstellt am 25.  1. 2006