Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon: Erläuterung zu

Konstruktion eines Potentials

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht
Besitzt ein Vektorfeld $ \vec{F}$ ein Potential $ U$, so kann dieses durch sukzessive Integration konstruiert werden. Bilden einer Stammfunktion bezüglich der ersten Variablen liefert

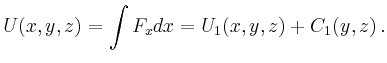
$\displaystyle U(x,y,z) = \int F_x dx = U_1(x,y,z)+C_1(y,z)\,. $

Nun folgt aus $ F_y = \partial_y U= \partial_y U_1 + \partial_y C_1$

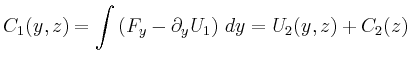
$\displaystyle C_1(y,z) = \int \left(F_y-\partial_y U_1 \right)\,dy = U_2(y,z) + C_2(z) $

und schließlich aus $ F_z = \partial_z U = \partial_z U_1 + \partial_z U_2 +\partial_z C_2$

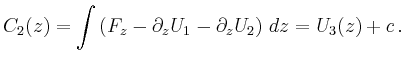
$\displaystyle C_2(z) = \int \left(F_z-\partial_zU_1 - \partial_z U_2\right)\,dz = U_3(z) + c\,. $

Insgesamt ergibt sich

$\displaystyle U(x,y,z) = U_1(x,y,z)+U_2(y,z)+U_3(z)+c\,. $

Ein Potential $ U$ eines Vektorfeldes $ \vec{F}(x,y,z) = \operatorname{grad} U$ kann auch mit Hilfe des Arbeitsintegrals bestimmt werden. Aufgrund der Wegunabhängigkeit des Arbeitsintegrals kann ein Weg von $ P$ nach $ Q$ gewählt werden, der parallel zu den Koordinatenachsen verläuft.

Wählt man den Weg, der zunächst parallel zur $ x$-, dann parallel zur $ y$- und zuletzt parallel zur $ z$-Achse verläuft, ergibt sich für das Potential das Hakenintegral

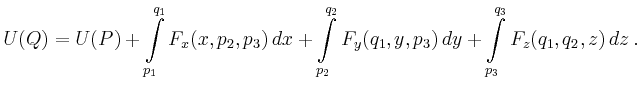
$\displaystyle U(Q)=U(P)+\int\limits_{p_1}^{q_1} F_x(x,p_2,p_3)\,dx + \int\limits_{p_2}^{q_2} F_y(q_1,y,p_3)\,dy +\int\limits_{p_3}^{q_3} F_z(q_1,q_2,z)\,dz\,. $



\includegraphics[clip, width=.6\linewidth]{aussage890_bild}

Durch Permutation der Koordinaten ergeben sich noch fünf weitere mögliche Hakenintegrale. Man wählt daraus dasjenige aus, bei dem die Integranden möglichst einfach werden. Meist ist es günstig, für $ P$ den Ursprung zu wählen.

Die Integrabilitätsbedingung $ \operatorname{rot}\vec{F}=\vec{0}$ garantiert, dass $ F_y-\partial_y U_1$ nicht von $ x$ und $ F_z -\partial_z U_1 -\partial_z U_2$ weder von $ x$ noch von $ y$ abhängt, die Definitionen von $ U_2$ und $ U_3$ also gerechtfertigt sind. Es ist nämlich

$\displaystyle \partial_x(F_y -\partial_y U_1) = \partial_x F_y - \partial_y \partial_x U_1 = \partial_x F_y - \partial_y F_x =0\,. $

Analog gilt

$\displaystyle \partial_x(F_z -\partial_z U_1 -\partial_z U_2) = \partial_x F_z... ...ial_x U_1 - \partial_z \partial_x U_2 = \partial_x F_z - \partial_z F_x -0 =0 $

und

$\displaystyle \partial_y(F_z -\partial_z U_1 -\partial_z U_2) = \partial_y F_z - \partial_z \partial_y (U_1 + U_2) = \partial_y F_z - \partial_z F_y =0\,. $

[Zurück]
  automatisch erstellt am 9. 10. 2013