
Mathematik-Online-Aufgabensammlung: Lösung zu

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |
|
Mathematik-Online-Aufgabensammlung: Lösung zu | |
Aufgabe 1394: komplexe hyperbolische Funktionen |
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z |
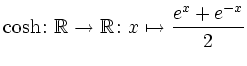 und
und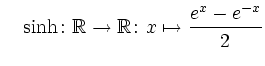
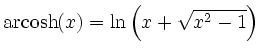 und
und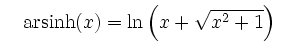 .
.
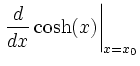 |
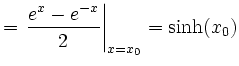 |
|
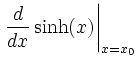 |
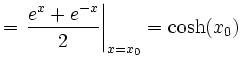 . . |
Die Funktion ![]() ist auf gesamt
ist auf gesamt
![]() streng monoton und
stetig mit dem Wertebereich
streng monoton und
stetig mit dem Wertebereich
![]() , deshalb existiert die
Umkehrfunktion
, deshalb existiert die
Umkehrfunktion
![]() ebenfalls auf gesamt
ebenfalls auf gesamt
![]() mit
dem Wertebereich
mit
dem Wertebereich
![]() .
.
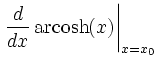 |
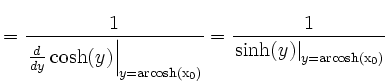 |
|
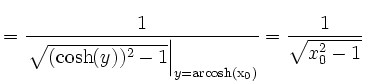 . . |
Da
![]() für alle
für alle
![]() ergibt sich aus obigem
Additionstheorem
ergibt sich aus obigem
Additionstheorem
Wieder liefert die Formel für die Ableitung der Umkehrfunktion
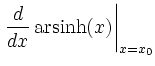 |
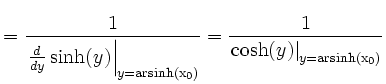 |
|
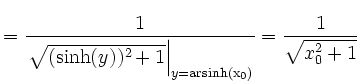 . . |
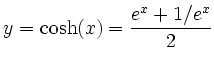
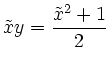 bzw.
bzw.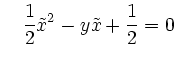
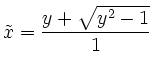 oder
oder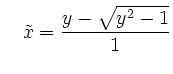
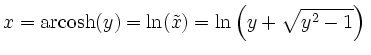 .
.
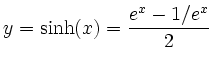
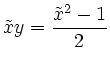 bzw.
bzw.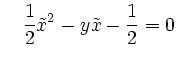 .
.
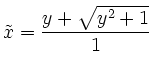 oder
oder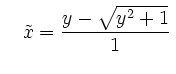 .
.
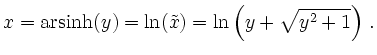
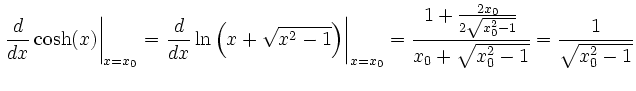
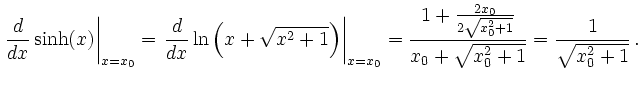
| automatisch erstellt am 28. 8. 2006 |