Mathematik-Online-Kurs: Lineare Algebra-Analytische Geometrie-Quadriken-Euklidische Normalform der dreidimensionalen Quadriken

	[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
	Mathematik-Online-Kurs: Lineare Algebra - Analytische Geometrie - Quadriken
	Euklidische Normalform der dreidimensionalen Quadriken

[vorangehende Seite] [nachfolgende Seite]

[Gesamtverzeichnis][Seitenübersicht]

Es existieren 17 verschiedene Typen räumlicher Quadriken mit folgenden Normalformen:

Kegelige Quadriken

Normalform Bezeichnung

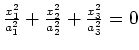$\frac{x_1^2}{a_1^2}+\frac{x_2^2}{a_2^2}+\frac{x_3^2}{a_3^2}=0$ Punkt

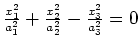$\frac{x_1^2}{a_1^2}+\frac{x_2^2}{a_2^2}-\frac{x_3^2}{a_3^2}=0$ (Doppel-)Kegel

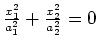$\frac{x_1^2}{a_1^2}+\frac{x_2^2}{a_2^2}=0$ Gerade

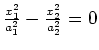$\frac{x_1^2}{a_1^2}-\frac{x_2^2}{a_2^2}=0$ schneidende Ebenen

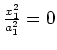$\frac{x_1^2}{a_1^2}=0$ Doppelebene

Mittelpunktsquadriken

Normalform	Bezeichnung
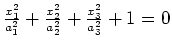$\frac{x_1^2}{a_1^2}+\frac{x_2^2}{a_2^2}+\frac{x_3^2}{a_3^2}+1=0$	(leere Menge)
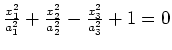$\frac{x_1^2}{a_1^2}+\frac{x_2^2}{a_2^2}-\frac{x_3^2}{a_3^2}+1=0$	zweischaliges Hyperboloid
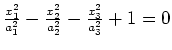$\frac{x_1^2}{a_1^2}-\frac{x_2^2}{a_2^2}-\frac{x_3^2}{a_3^2}+1=0$	einschaliges Hyperboloid
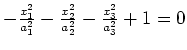$-\frac{x_1^2}{a_1^2}-\frac{x_2^2}{a_2^2}-\frac{x_3^2}{a_3^2}+1=0$	Ellipsoid
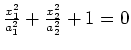$\frac{x_1^2}{a_1^2}+\frac{x_2^2}{a_2^2}+1=0$	(leere Menge)
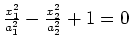$\frac{x_1^2}{a_1^2}-\frac{x_2^2}{a_2^2}+1=0$	hyperbolischer Zylinder
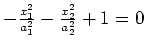$-\frac{x_1^2}{a_1^2}-\frac{x_2^2}{a_2^2}+1=0$	elliptischer Zylinder
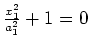$\frac{x_1^2}{a_1^2}+1=0$	(leere Menge)
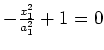$-\frac{x_1^2}{a_1^2}+1=0$	parallele Ebenen

Parabolische Quadriken

Normalform Bezeichnung

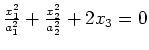$\frac{x_1^2}{a_1^2}+\frac{x_2^2}{a_2^2}+2x_3=0$ elliptisches Paraboloid

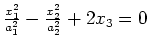$\frac{x_1^2}{a_1^2}-\frac{x_2^2}{a_2^2}+2x_3=0$ hyperbolisches Paraboloid

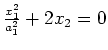$\frac{x_1^2}{a_1^2}+2x_2=0$ parabolischer Zylinder

Die Normalformen sind eindeutig bis auf Permutation der Indizes und bei kegeligen Quadriken bis auf Multiplikation mit einer Konstanten $c\ne 0$ . Die Größen werden positiv angesetzt und heißen Hauptachsenlängen der Quadrik.

(Doppel-)Kegel	schneidende Ebenen

$\includegraphics[width=.4\moimagesize]{quadriken_kegel}$	$\includegraphics[width=.4\moimagesize]{quadriken_schneidende_ebenen}$

zweischaliges Hyperboloid	einschaliges Hyperboloid

$\includegraphics[width=.4\moimagesize]{quadriken_zweischaliges_hyperboloid}$	$\includegraphics[width=.4\moimagesize]{quadriken_einschaliges_hyperboloid}$

Ellipsoid	hyperbolischer Zylinder

$\includegraphics[width=.4\moimagesize]{quadriken_ellipsoid}$	$\includegraphics[width=.4\moimagesize]{quadriken_hyperbolischer_zylinder}$

elliptischer Zylinder	elliptisches Paraboloid

$\includegraphics[width=.4\moimagesize]{quadriken_elliptischer_zylinder}$	$\includegraphics[width=.4\moimagesize]{quadriken_paraboloid}$

hyperbolisches Paraboloid	parabolischer Zylinder

$\includegraphics[width=.4\moimagesize]{quadriken_hyperbolisches_paraboloid}$	$\includegraphics[width=.4\moimagesize]{quadriken_parabolischer_zylinder}$

Es soll die Normalform und der Typ der Quadrik

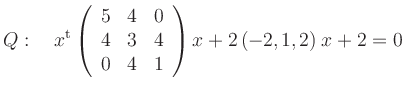
$\displaystyle Q: \quad x^{\operatorname t}\left(\begin{array}{rrr}5 & 4 & 0 \\ 4 & 3 & 4 \\ 0 & 4 & 1\end{array}\right)x+2 \left(-2,1,2\right)x+2=0$

bestimmt werden.

Das charakteristische Polynom der Matrix,

$\displaystyle p(\lambda)=\lambda^3-9\lambda^2-9\lambda+81\,,$

hat die Nullstellen

$\displaystyle \lambda_1=9\,,\quad \lambda_2=3\,,\quad \lambda_3=-3\,.$

Entsprechende normierte Eigenvektoren zu den Eigenwerten $\lambda_i$ sind

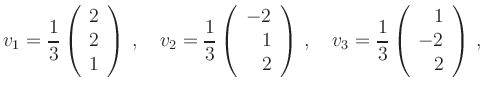
$\displaystyle v_1=\frac{1}{3}\left(\begin{array}{r}2\\ 2\\ 1\end{array}\right)\... ...)\,,\quad v_3=\frac{1}{3}\left(\begin{array}{r}1\\ -2\\ 2\end{array}\right)\,,$

wobei die Vorzeichen so gewählt sind, dass ein Rechtssystem entsteht. Als orthogonale Transformationsmatrix erhält man

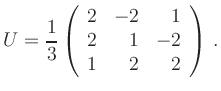
$\displaystyle U=\frac{1}{3}\left(\begin{array}{rrr} 2 & -2 & 1\\ 2 & 1 &-2\\ 1&2&2\end{array}\right)\,.$

Die mit

transformierte Gleichung hat die Form

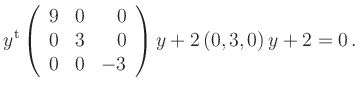
$\displaystyle y^{\operatorname t}\left(\begin{array}{rrr}9 & 0 & 0 \\ 0 & 3 & 0 \\ 0 & 0 & -3\end{array}\right)y+2 \left(0,3,0\right)y+2=0\,.$

Quadratisches Ergänzen liefert

0	$\displaystyle =$	$\displaystyle 9y_1^2+3y_2^2-3y_3^2+6y_2+2$
	$\displaystyle =$	$\displaystyle 9y_1^2+3(y_2+1)^2-6y_2-3-3y_3^2+6y_2+2$
	$\displaystyle =$	$\displaystyle 9z_1^2+3z_2^2-3z_3^2-1$

beziehungsweise

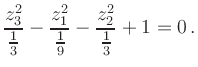
$\displaystyle \frac{z_3^2}{\frac{1}{3}}-\frac{z_1^2}{\frac{1}{9}}-\frac{z_2^2}{\frac{1}{3}}+1=0\,.$

Die Gleichung stellt also ein einschaliges Hyperboloid mit Hauptachsenlängen

$\displaystyle a_3 = \sqrt{1/3},\quad a_1 = 1/3,\quad a_2 = \sqrt{1/3}$

und Mittelpunkt

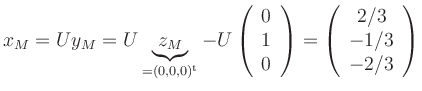
$\displaystyle x_M = U y_M = U\underbrace{z_M}_{=(0,0,0)^{\text{t}}} - U \left(... ...nd{array}\right) = \left(\begin{array}{c}2/3\\ -1/3\\ -2/3\end{array}\right)$

dar.

[vorangehende Seite] [nachfolgende Seite]

[Gesamtverzeichnis][Seitenübersicht]

automatisch erstellt am 14.6.2012

Normalform	Bezeichnung
$\frac{x_1^2}{a_1^2}+\frac{x_2^2}{a_2^2}+\frac{x_3^2}{a_3^2}=0$	Punkt
$\frac{x_1^2}{a_1^2}+\frac{x_2^2}{a_2^2}-\frac{x_3^2}{a_3^2}=0$	(Doppel-)Kegel
$\frac{x_1^2}{a_1^2}+\frac{x_2^2}{a_2^2}=0$	Gerade
$\frac{x_1^2}{a_1^2}-\frac{x_2^2}{a_2^2}=0$	schneidende Ebenen
$\frac{x_1^2}{a_1^2}=0$	Doppelebene