

Mathematik-Online-Kurs: Mathematische Grundlagen - Natürliche Zahlen

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |

|
|
Mathematik-Online-Kurs: Mathematische Grundlagen - Natürliche Zahlen | ||
Vollständige Induktion | ||
| [vorangehende Seite] [nachfolgende Seite] | [Gesamtverzeichnis][Seitenübersicht] |
Aussageformen mit natürlichen Zahlen als Parametern
kann man mit vollständiger Induktion beweisen.
Ist ![]() eine von
eine von
![]() abhängige
Aussage, so sind dazu die folgenden beiden
Beweisschritte durchzuführen.
abhängige
Aussage, so sind dazu die folgenden beiden
Beweisschritte durchzuführen.
Bei einem Induktionsbeweis wird sukzessive das
Nächste aus dem Vorherigen gefolgert.
Wird der Induktionsanfang
nicht für ![]() ,
sondern für ein
,
sondern für ein ![]() durchgeführt, so
gilt die
Aussage nur für alle
durchgeführt, so
gilt die
Aussage nur für alle
![]() .
.
Die Formel für die Summe der Quadratzahlen,
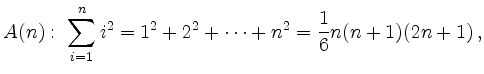
Induktionsanfang (![]() ):
):
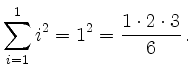
Induktionsschluß (
![]() :
:
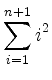 |
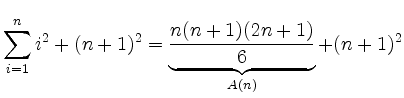 |
||
![$\displaystyle \displaystyle\frac{(n+1)\big[n(2n+1)+6(n+1)\big]}{6}
= \displaystyle\frac{(n+1)(n+2)(2n+3)}{6}\,.$](/inhalt/beispiel/beispiel52/img8.png) |
| [vorangehende Seite] [nachfolgende Seite] | [Gesamtverzeichnis][Seitenübersicht] |
| automatisch erstellt am 5.5.2011 |