

Mathematik-Online-Kurs: Mathematische Grundlagen - Kombinatorik

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |

|
|
Mathematik-Online-Kurs: Mathematische Grundlagen - Kombinatorik | ||
Binomischer Lehrsatz | ||
| [vorangehende Seite] [nachfolgende Seite] | [Gesamtverzeichnis][Seitenübersicht] |
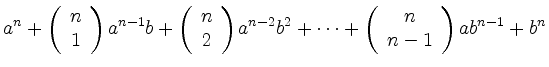 |
|||
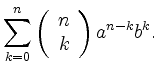 |
Der binomische Lehrsatz kann mit vollständiger Induktion bewiesen werden.
Für ![]() und
und ![]() ist die Identität wegen
ist die Identität wegen
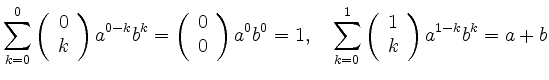
Angenommen sie gelte für ![]() . Dann ist
. Dann ist
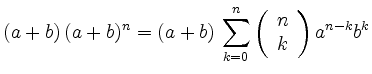 |
|||
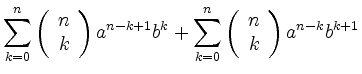 |
|||
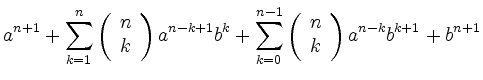 |
|||
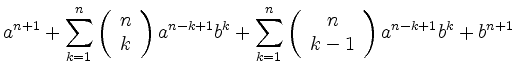 |
|||
![$\displaystyle a^{n+1} + \sum_{k=1}^n \left[
\left( \begin{array}{c} n \\ k \end...
...eft( \begin{array}{c} n \\ k-1 \end{array}\right)\right]
a^{n+1-k}b^k + b^{n+1}$](/inhalt/erlaeuterung/erlaeuterung40/img13.png) |
|||
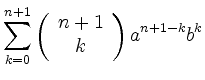 |
| [vorangehende Seite] [nachfolgende Seite] | [Gesamtverzeichnis][Seitenübersicht] |
| automatisch erstellt am 5.5.2011 |