

Mathematik-Online-Kurs: Vorkurs Mathematik - Lineare Algebra und Geometrie - Elementare Geometrie: Dreiecke

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |

|
|
Mathematik-Online-Kurs: Vorkurs Mathematik - Lineare Algebra und Geometrie - Elementare Geometrie: Dreiecke | ||
Satz von Pythagoras | ||
| [vorangehende Seite] [nachfolgende Seite] | [Gesamtverzeichnis][Seitenübersicht] |
![\includegraphics[width=.7\moimagesize]{pythagoras_bild}](/inhalt/aussage/aussage366/img1.png)
In dem Quadrat über der Hypotenuse mit
Flächeninhalt ![]() lassen sich
4 zum Originaldreieck kongruente Dreiecke
einzeichnen.
lassen sich
4 zum Originaldreieck kongruente Dreiecke
einzeichnen.
![\includegraphics[width=.6\moimagesize]{b_pythagoras_bild}](/inhalt/erlaeuterung/erlaeuterung135/img2.png)
Da
![]() ist,
treten dabei an den Ecken
keine Überschneidungen auf.
Addiert man die Flächeninhalte der Dreiecke und
des kleineren Quadrates in der Mitte mit
Seitenlänge
ist,
treten dabei an den Ecken
keine Überschneidungen auf.
Addiert man die Flächeninhalte der Dreiecke und
des kleineren Quadrates in der Mitte mit
Seitenlänge ![]() , so ergibt sich
, so ergibt sich
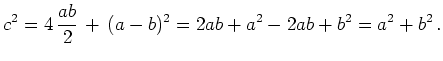
| [vorangehende Seite] [nachfolgende Seite] | [Gesamtverzeichnis][Seitenübersicht] |
| automatisch erstellt am 23.10.2009 |