Es sind die folgenden Funktionen gegeben:
Bestimmen Sie mit Hilfe der Intervallhalbierungsmethode, falls möglich,
jeweils eine Nullstelle im Intervall ![$ [-1,3]$](/inhalt/aufgabe/aufgabe1421/img5.png) und im Intervall
und im Intervall ![$ [0,2]$](/inhalt/aufgabe/aufgabe1421/img6.png) . Geben
sie die Nullstellen
. Geben
sie die Nullstellen 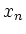 bis auf eine Genauigkeit von
bis auf eine Genauigkeit von 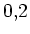 an, das heißt:
Es gibt ein
an, das heißt:
Es gibt ein
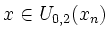 so, dass
so, dass 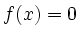 respektive
respektive 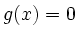 .
.
Zusatz: Bestimmen Sie alle Nullstellen von 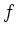 und
und
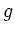 bis auf eine Genauigkeit von
bis auf eine Genauigkeit von 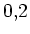 . Skizzieren Sie deren
Graphen und bestimmen Sie deren Wertebereiche. Dazu reicht Ihr Wissen aus der
Vorlesung und das Wissen, das Sie sich in der Schule zum Erwerb der
allgemeinen Hochschulreife angeeignet haben.
. Skizzieren Sie deren
Graphen und bestimmen Sie deren Wertebereiche. Dazu reicht Ihr Wissen aus der
Vorlesung und das Wissen, das Sie sich in der Schule zum Erwerb der
allgemeinen Hochschulreife angeeignet haben.
(Aus: HM II Stroppel SS 2006)
| |
automatisch erstellt
am 25. 8. 2006 |


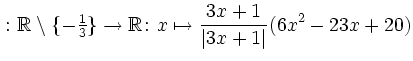
![]() und
und
![]() bis auf eine Genauigkeit von
bis auf eine Genauigkeit von ![]() . Skizzieren Sie deren
Graphen und bestimmen Sie deren Wertebereiche. Dazu reicht Ihr Wissen aus der
Vorlesung und das Wissen, das Sie sich in der Schule zum Erwerb der
allgemeinen Hochschulreife angeeignet haben.
. Skizzieren Sie deren
Graphen und bestimmen Sie deren Wertebereiche. Dazu reicht Ihr Wissen aus der
Vorlesung und das Wissen, das Sie sich in der Schule zum Erwerb der
allgemeinen Hochschulreife angeeignet haben.