Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Beschränkter linearer Operator

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht
Eine lineare Abbildung

$\displaystyle L:\quad V\rightarrow W $

zwischen zwei normierten Vektorräumen heißt beschränkter linearer Operator, wenn die Operatornorm

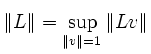
$\displaystyle \Vert L\Vert=\sup_{\Vert v\Vert=1}\Vert Lv\Vert $

endlich ist. Die Beschränktheit ist gleichbedeutend mit der Stetigkeit von $ L$ .

Man verwendet die Bezeichnung linearer Operator an Stelle der in der linearen Algebra üblichen Bezeichnung lineare Abbildung, um den unendlich-dimensionalen Kontext hervorzuheben.

Der Raum aller beschränkter linearer Operatoren von $ V$ nach $ W$ wird mit $ \mathcal{L}(V,W)$ bezeichnet. Er ist ein Banach-Raum, wenn $ W$ ein Banach-Raum ist.

siehe auch:

[Beispiele]
  automatisch erstellt am 19.  8. 2013