Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Körper

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Ein Körper ist eine Menge $ \mbox{$K$}$ zusammen mit Operationsabbildungen

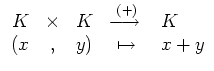
$ \mbox{$\displaystyle \begin{array}{rclcl} K & \times & K & \unitlength.1mm\be... ... (+)$}} \end{picture} & K \\ (x & , & y) & \mapsto & x + y \\ \end{array}$}$
und
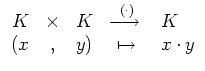
$ \mbox{$\displaystyle \begin{array}{rclcl} K & \times & K & \unitlength.1mm\be... ...$}} \end{picture} & K \\ (x & , & y) & \mapsto & x \cdot y \\ \end{array}$}$
so, daß für $ \mbox{$x,y,z\in K$}$ folgende Regeln gelten.

Die neutralen und inversen Elemente der Addition und Multiplikation sind eindeutig bestimmt.

Die Menge der natürlichen Zahlen $ \mbox{$\mathbb{N}= \{0,1,2,3,4,\dots\}$}$ bildet mit Addition und Multiplikation keinen Körper, da z.B. $ \mbox{$1$}$ in $ \mbox{$\mathbb{N}$}$ kein additiv Inverses besitzt.

Ebenfalls bildet die Menge der ganzen Zahlen $ \mbox{$\mathbb{Z}= \{\dots,-3,-2,-1,0,1,2,3,\dots\}$}$ mit Addition und Multiplikation keinen Körper, da z.B. $ \mbox{$2$}$ in $ \mbox{$\mathbb{Z}$}$ kein multiplikativ Inverses besitzt.

Dahingegen bildet die Menge der rationalen Zahlen $ \mbox{$\mathbb{Q}= \{\frac{a}{b} \; :\; a,b\in\mathbb{Z},\; b\neq 0\}$}$ mit Addition und Multiplikation einen Körper.

Die Menge der unendlichen Dezimalbrüche der Form

$ \mbox{$\displaystyle \pm \alpha_n \dots \alpha_1\, \alpha_0\, , \, \alpha_{-1}\,\alpha_{-2}\,\alpha_{-3}\dots $}$
mit $ \mbox{$\alpha_i\in\{ 0,1,2,\dots,9\}$}$ bildet den Körper $ \mbox{$\mathbb{R}$}$ der reellen Zahlen. Periode $ \mbox{$9$}$ sei hierbei ausgeschlossen und durch die `Aufrundung' (um $ \mbox{$0$}$) zu ersetzen. Z.B. schreibt man statt $ \mbox{$0.1999\ldots$}$ vereinbarungsgemäß $ \mbox{$0.2$}$.

Darin findet man die rationalen Zahlen als Teilmenge der abbrechenden oder periodischen Dezimalbrüche.

Zum Beispiel sind

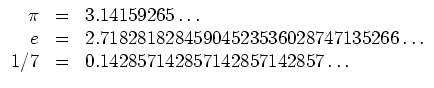
$ \mbox{$\displaystyle \begin{array}{rcl} \pi & = & 3.14159265\dots \\ e & = ... ...028747135266\dots \\ 1/7 & = & 0.142857142857142857142857 \dots \end{array}$}$
reelle Zahlen, letzteres ist sogar eine rationale Zahl.

Zur Definition des Körpers der komplexen Zahlen führen wir eine formale Quadratwurzel aus $ \mbox{$-1$}$ ein und bezeichnen diese mit $ \mbox{$\mathrm{i}$}$. Dann gilt $ \mbox{$\mathrm{i}^2 = (-\mathrm{i})^2 = -1$}$ und allgemeiner, mit $ \mbox{$x,y,x',y'\in\mathbb{R}$}$,

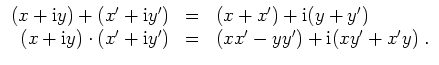
$ \mbox{$\displaystyle \begin{array}{rcl} (x + \mathrm{i}y) + (x' + \mathrm{i}y... ... \mathrm{i}y') & = & (xx' - yy') + \mathrm{i}(xy' + x'y)\; . \\ \end{array}$}$
Mit dieser Addition und dieser Multiplikation wird die Menge der komplexen Zahlen, d.h. die Menge der formalen Summen
$ \mbox{$\displaystyle \mathbb{C}\; :=\; \{ x + \mathrm{i}y \; :\; x,y\in \mathbb{R}\} \\ $}$
zu einem Körper. Ist $ \mbox{$z = x + \mathrm{i}y\in\mathbb{C}$}$, $ \mbox{$x,y\in\mathbb{R}$}$, eine komplexe Zahl, so heißt $ \mbox{${\operatorname{Re}}(z) := x$}$ der Realteil und $ \mbox{${\operatorname{Im}}(z) := y$}$ der Imaginärteil von $ \mbox{$z$}$. Speziell findet man $ \mbox{$\mathbb{R}$}$ als Teilmenge der komplexen Zahlen mit Imaginärteil Null.

Die konjugiert komplexe Zahl zu $ \mbox{$z = x + \mathrm{i}y$}$ ist durch

$ \mbox{$\displaystyle \bar z \; =\; x -\mathrm{i}y $}$
definiert. Es gilt $ \mbox{$\overline{z + z'} = \bar z + \overline {z'}$}$ und $ \mbox{$\overline{zz'} = \overline {z} \cdot \overline {z'}$}$ für $ \mbox{$z,z'\in\mathbb{C}$}$.

Der Betrag von $ \mbox{$z = x + \mathrm{i}y$}$ ist definiert als

$ \mbox{$\displaystyle \vert z\vert \; =\; \sqrt{x^2 + y^2} \; =\; \sqrt{z \bar z}\; . $}$
Es gilt $ \mbox{$\vert z z'\vert = \vert z\vert\vert z'\vert$}$. Additiv gilt nur die sogenannte Dreiecksungleichung
$ \mbox{$\displaystyle \vert z + z'\vert\;\leq\; \vert z\vert + \vert z'\vert\; . $}$
Hieraus folgt
$ \mbox{$\displaystyle \vert z \pm z'\vert\;\geq\; \vert\vert z\vert - \vert z'\vert\vert\; . $}$

Geometrisch kann eine komplexe Zahl $ \mbox{$z = x + \mathrm{i}y$}$ in der Gaußschen Zahlenebene dargestellt werden als ein Vektor mit den Koordinaten $ \mbox{$\left(\begin{matrix}x \\ y \end{matrix}\right)$}$ und der Länge $ \mbox{$\vert z\vert = \sqrt{x^2 + y^2}$}$.


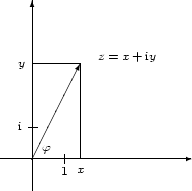
\begin{picture}(100,120) \put( -20, 20){\vector(1,0){120}} \put( 20, 17){\line(0... ...( 41, 82){{$\mbox{$\scriptstyle z \; =\; x \, + \,\mathrm{i}y$}$}} \end{picture}

Die Addition entspricht der Vektoraddition (Aneinandersetzen der Pfeile). Bei der Multiplikation addieren sich die mit der reellen Achse eingeschlossenen Winkel ( $ \mbox{$\varphi $}$ im Bild), und die Beträge multiplizieren sich.

(Autoren: Künzer/Martin/Nebe)

siehe auch:

[Beispiele]
  automatisch erstellt am 25.  1. 2006