Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Binomialkoeffizienten

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Für jede natürliche Zahl $ \mbox{$n$}$ ist die Fakultät von $ \mbox{$n$}$ definiert durch

$ \mbox{$\displaystyle n!\; :=\; \prod_{j = 1}^n j \; =\; 1\cdot 2\cdots (n-1)\cdot n. $}$
Das leere Produkt wird als $ \mbox{$1$}$ definiert; daher gilt $ \mbox{$0!=1$}$. Stets gilt $ \mbox{$(n+1)!=n!\cdot(n+1)$}$.

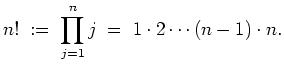
Kombinatorisch ist $ \mbox{$n!$}$ die Anzahl der Möglichkeiten, die Zahlen $ \mbox{$\{1,\dots, n\}$}$ anzuordnen (d.h. die Anzahl der Bijektionen von $ \mbox{$\{1,\dots, n\}$}$ nach $ \mbox{$\{1,\dots, n\}$}$).

Für jede komplexe Zahl $ \mbox{$z$}$ und jede natürliche Zahl $ \mbox{$k$}$ ist der Binomialkoeffizient von $ \mbox{$z$}$ über $ \mbox{$k$}$ definiert durch

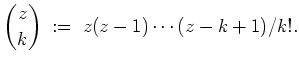
$ \mbox{$\displaystyle {z\choose k}\; :=\; z(z-1)\cdots (z-k+1)/k!. $}$
Ist $ \mbox{$n$}$ eine natürliche Zahl mit $ \mbox{$0\leq k\leq n$}$, so gilt
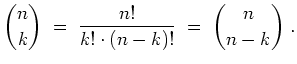
$ \mbox{$\displaystyle {n\choose k} \; =\; \frac{n!}{k!\cdot (n-k)!}\; =\; {n\choose n-k}\; . $}$
Kombinatorisch ist $ \mbox{$n\choose k$}$ die Anzahl der Möglichkeiten, $ \mbox{$k$}$ Zahlen aus $ \mbox{$\{1,\dots, n\}$}$ auszuwählen (d.h. die Anzahl der Teilmengen von $ \mbox{$\{1,\dots, n\}$}$, die $ \mbox{$k$}$ Elemente enthalten).

Für $ \mbox{$z\in\mathbb{C}$}$ und $ \mbox{$k\in\mathbb{N}$}$ gelten die folgenden Rechenregeln für Binomialkoeffizienten:

Die letzte Rechenregel ergibt sich wie folgt.

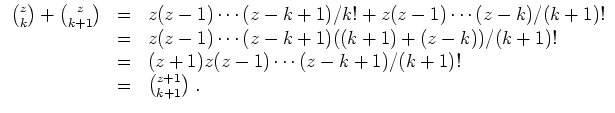
$ \mbox{$\displaystyle \begin{array}{rcl} {z\choose k} + {z\choose k+1} & = & z... ...z-1)\cdots (z-k+1)/(k+1)!  \\ & = & {z+1 \choose k+1}\; .  \\ \end{array}$}$

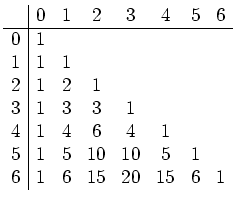
Aus dieser Rechenregel ergibt sich das folgende Pascalsche Dreieck für $ \mbox{${n \choose k}$}$ für kleine natürliche $ \mbox{$n$}$ und $ \mbox{$k$}$, wobei $ \mbox{$n$}$ die Zeilen und $ \mbox{$k$}$ die Spalten zählt.

$ \mbox{$\displaystyle \begin{array}{c\vert ccccccc} & 0 & 1 & 2 & 3 & 4 & 5 &... ... 5 & 10 & 10 & 5 & 1 & \\ 6 & 1 & 6 & 15 & 20 & 15 & 6 & 1 \\ \end{array}$}$

Für $ \mbox{$x,y$}$ aus einem beliebigen Körper $ \mbox{$K$}$ (z.B. $ \mbox{$K =\mathbb{R}$}$ oder $ \mbox{$K = \mathbb{C}$}$) und $ \mbox{$m\in\mathbb{N}$}$ gilt die binomische Formel

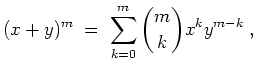
$ \mbox{$\displaystyle (x + y)^m \; =\; \sum_{k = 0}^m {m\choose k} x^k y^{m-k}\; , $}$
da beim Ausmultiplizieren der Summand $ \mbox{$x^k y^{m-k}$}$ so oft entsteht, wie man $ \mbox{$k$}$ Faktoren aus allen $ \mbox{$m$}$ Faktoren auswählen kann.

Zum Beispiel ist $ \mbox{$\sum_{k = 0}^m {m\choose k} = \sum_{k = 0}^m {m\choose k} 1^k 1^{m-k} = (1 + 1)^m = 2^m$}$, wie man im Pascalschen Dreieck verifiziere.

(Autoren: Künzer/Martin/Nebe)

siehe auch:

[Beispiele]
  automatisch erstellt am 25.  1. 2006