Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Funktionen

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Funktionen allgemein.

Seien $ \mbox{$X$}$ und $ \mbox{$Y$}$ zwei Mengen. Eine Funktion (auch Abbildung genannt) ist eine Vorschrift

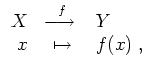
$ \mbox{$\displaystyle \begin{array}{rcl} X & \unitlength.1mm\begin{picture}(80... ...riptstyle f$}} \end{picture} & Y \\ x & \mapsto & f(x)\; , \\ \end{array}$}$
die jedem Element $ \mbox{$x\in X$}$ ein Bildelement $ \mbox{$f(x)\in Y$}$ zuordnet.

Sei das cartesische Produkt $ \mbox{$X\times Y$}$ von $ \mbox{$X$}$ und $ \mbox{$Y$}$ definiert als

$ \mbox{$\displaystyle X \times Y \; :=\; \{ (x,y) \; \vert\; x\in X,\; y\in Y\} \; . $}$

Formal kann man Funktionen auch über den Graphen $ \mbox{$\Gamma(f) := \{ (x,f(x))\; \vert\; x\in X\}\subseteq X\times Y$}$ von $ \mbox{$f$}$ einführen - ein Funktionsgraph ist eine Teilmenge $ \mbox{$\Gamma$}$ von $ \mbox{$X\times Y$}$ derart, daß für jedes $ \mbox{$x\in X$}$ genau ein $ \mbox{$y\in Y$}$ mit $ \mbox{$(x,y)\in\Gamma$}$ existiert.

Sei $ \mbox{$X\unitlength.1mm\begin{picture}(80,50) \put( 0, 0){$\longrightarrow $} \put( 10, 27){\makebox[6mm]{$\scriptstyle f$}} \end{picture} Y$}$, und seien $ \mbox{$U\subseteq X$}$ und $ \mbox{$V\subseteq Y$}$ Teilmengen. Wir definieren das Bild $ \mbox{$f(U)$}$ und das Urbild $ \mbox{$f^{-1}(V)$}$ via

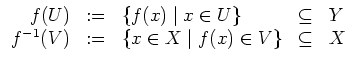
$ \mbox{$\displaystyle \begin{array}{rclcl} f(U) & := & \{f(x)\; \vert\; x\in U... ...-1}(V) & := & \{x\in X\; \vert\; f(x)\in V\} & \subseteq & X \\ \end{array}$}$

Ist $ \mbox{$M$}$ eine Menge, so bezeichnen wir die Anzahl ihrer Elemente mit $ \mbox{$\char93 M$}$. Ist $ \mbox{$M$}$ eine unendliche Menge, so schreiben wir $ \mbox{$\char93 M = \infty$}$.

Die Funktion $ \mbox{$f$}$ heißt injektiv, wenn $ \mbox{$\char93 f^{-1}(\{ y\}) \leq 1$}$ für alle $ \mbox{$y\in Y$}$.

Die Funktion $ \mbox{$f$}$ heißt surjektiv, wenn $ \mbox{$\char93 f^{-1}(\{ y\}) \geq 1$}$ für alle $ \mbox{$y\in Y$}$.

Die Funktion $ \mbox{$f$}$ heißt bijektiv, wenn $ \mbox{$\char93 f^{-1}(\{ y\}) = 1$}$ für alle $ \mbox{$y\in Y$}$. Diesenfalls schreiben wir auch $ \mbox{$f^{-1}(y) = x$}$ für $ \mbox{$f^{-1}(\{ y\}) = \{ x\}$}$, und $ \mbox{$Y\unitlength.1mm\begin{picture}(80,50) \put( 0, 0){$\longrightarrow $} \put( 10, 27){\makebox[6mm]{$\scriptstyle f^{-1}$}} \end{picture} X$}$ definiert ebenfalls eine bijektive Funktion, genannt die Umkehrabbildung zu $ \mbox{$f$}$.

Vorsicht. Bezüglich jeder Funktion kann man Urbilder von Teilmengen nehmen. Es haben aber nur bijektive Funktionen eine Umkehrfunktion.

Kurz, $ \mbox{$f$}$ ist injektiv, falls verschiedene Elemente auf verschiedene Bildelemente gehen. Und $ \mbox{$f$}$ ist surjektiv, falls $ \mbox{$f(X) = Y$}$.

Seien $ \mbox{$X\unitlength.1mm\begin{picture}(80,50) \put( 0, 0){$\longrightarrow $} \put( 10, 27){\makebox[6mm]{$\scriptstyle f$}} \end{picture} Y$}$ und $ \mbox{$Y\unitlength.1mm\begin{picture}(80,50) \put( 0, 0){$\longrightarrow $} \put( 10, 27){\makebox[6mm]{$\scriptstyle g$}} \end{picture} Z$}$ Funktionen. Wir definieren die Verkettung $ \mbox{$g\circ f$}$ (gesprochen « $ \mbox{$g$}$ nach $ \mbox{$f$}$») als

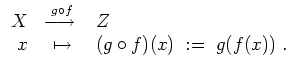
$ \mbox{$\displaystyle \begin{array}{rcl} X & \unitlength.1mm\begin{picture}(80... ...ure} & Z \\ x & \mapsto & (g\circ f)(x) \; :=\; g(f(x))\; .\\ \end{array}$}$

Ist $ \mbox{$X\unitlength.1mm\begin{picture}(80,50) \put( 0, 0){$\longrightarrow $} \put( 10, 27){\makebox[6mm]{$\scriptstyle f$}} \end{picture} Y$}$ bijektiv, so ist $ \mbox{$f\circ f^{-1}={\rm id}_Y$}$ und $ \mbox{$f^{-1}\circ f={\rm id}_X$}$, wobei $ \mbox{${\rm id}_X:X\longrightarrow X,\; x\mapsto x$}$ die identische Abbildung auf $ \mbox{$X$}$ bezeichnet.

Sind sowohl $ \mbox{$f:X\longrightarrow Y$}$ und $ \mbox{$g:Y\longrightarrow Z$}$ bijektiv, so ist auch die Verkettung $ \mbox{$g\circ f:X\longrightarrow Z$}$ bijektiv, und es gilt

$ \mbox{$\displaystyle (g\circ f)^{-1}\; =\; f^{-1} \circ g^{-1}\; . $}$

Reelle Funktionen (eindimensional).

Ist $ \mbox{$X = D \subseteq \mathbb{R}$}$ und $ \mbox{$Y = \mathbb{R}$}$, so sprechen wir von einer (eindimensionalen) reellen Funktion $ \mbox{$D\unitlength.1mm\begin{picture}(80,50) \put( 0, 0){$\longrightarrow $} \put( 10, 27){\makebox[6mm]{$\scriptstyle f$}} \end{picture} \mathbb{R}$}$.

Es sei $ \mbox{$f:D\longrightarrow \mathbb{R}$}$ eine Funktion mit Definitionsbereich $ \mbox{$D\subseteq\mathbb{R}$}$.

$ \mbox{$f$}$ heißt monoton wachsend (bzw. monoton fallend), falls für $ \mbox{$x,y\in D$}$ mit $ \mbox{$x\leq y$}$ stets $ \mbox{$f(x)\leq f(y)$}$ (bzw. $ \mbox{$f(x)\geq f(y)$}$) gilt.

$ \mbox{$f$}$ heißt streng monoton wachsend (bzw. streng monoton fallend), falls für $ \mbox{$x,y\in D$}$ mit $ \mbox{$x<y$}$ stets $ \mbox{$f(x)<f(y)$}$ (bzw. $ \mbox{$f(x)>f(y)$}$) gilt.

$ \mbox{$f$}$ heißt monoton, falls sie monoton wachsend oder monoton fallend ist.

$ \mbox{$f$}$ heißt streng monoton, falls sie streng monoton wachsend oder streng monoton fallend ist.

Die Funktion $ \mbox{$f:D\longrightarrow \mathbb{R}$}$ heißt nach oben beschränkt (bzw. nach unten beschränkt), falls es ein $ \mbox{$a\in\mathbb{R}$}$ gibt mit $ \mbox{$f(x)\leq a$}$ (bzw. $ \mbox{$f(x)\geq a$}$) für alle $ \mbox{$x \in D$}$. Sie heißt beschränkt, falls sie sowohl nach oben als auch nach unten beschränkt ist.

Sind $ \mbox{$f$}$ und $ \mbox{$g$}$ reelle Funktionen mit demselben Definitionsbereich $ \mbox{$D\subseteq\mathbb{R}$}$, so definieren wir auch die folgenden Funktionen.

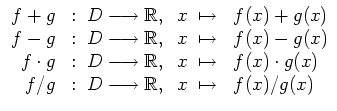
$ \mbox{$\displaystyle \begin{array}{rcl} f+g & :\; D\longrightarrow \mathbb{R}... ... :\; D\longrightarrow \mathbb{R}, \;\; x\;\mapsto & f(x)/g(x)\\ \end{array}$}$

Für die Bildung von $ \mbox{$f/g$}$ müssen wir natürlich voraussetzen, daß $ \mbox{$g(x)\ne 0$}$ für alle $ \mbox{$x\in D$}$.

Seien $ \mbox{$a,b\in\mathbb{R}$}$, $ \mbox{$a\leq b$}$. Als Definitionsbereich reeller Funktionen treten häufig Intervalle der folgenden Form auf.

$ \mbox{$\displaystyle \begin{array}{rcl} {[a,b]} & := & \{ x\in\mathbb{R}\; \v... ...\ {(-\infty,b)} & := & \{ x\in\mathbb{R}\; \vert\; x < b\} \\ \end{array}$}$
Man schreibt auch $ \mbox{$\mathbb{R}_{> 0} := (0,\infty)$}$ usf.

Polynome und rationale Funktionen.

Ein (reelles) Polynom ist eine Funktion der Form

$ \mbox{$\displaystyle f:\mathbb{R}\longrightarrow \mathbb{R},\; x\mapsto f(x) = a_0 + a_1 x + a_2 x^2 + \cdots + a_n x^n\; , $}$
wobei $ \mbox{$a_0,\ldots,a_n$}$ reelle Zahlen sind. Die Koeffizienten $ \mbox{$a_0,\ldots,a_n$}$ von $ \mbox{$f$}$ sind eindeutig bestimmt, d.h. zwei Polynomdarstellungen ein und derselben Funktion weisen dieselben Koeffizienten auf.

Ist $ \mbox{$a_n\ne 0$}$, so heißt $ \mbox{$\deg(f):=n$}$ der Grad des Polynoms $ \mbox{$f$}$. Sind alle Koeffizienten gleich $ \mbox{$0$}$, so heißt $ \mbox{$f$}$ das Nullpolynom, geschrieben $ \mbox{$f=0$}$, und man definiert $ \mbox{$\deg(0):=-\infty$}$.

Sind $ \mbox{$f$}$ und $ \mbox{$g\neq 0$}$ zwei Polynome, so können wir $ \mbox{$f$}$ durch $ \mbox{$g$}$ mit Rest teilen. Wir finden durch diese Polynomdivision Polynome $ \mbox{$s$}$ und $ \mbox{$t$}$ mit $ \mbox{$\deg(t) < \deg(g)$}$ und

$ \mbox{$\displaystyle f \; =\; sg + t\; . $}$

Sind $ \mbox{$f$}$ und $ \mbox{$g$}$ zwei Polynome, so wird der Quotient $ \mbox{$r(x):=f(x)/g(x)$}$ als rationale Funktion bezeichnet, definiert auf $ \mbox{$\{ x\in\mathbb{R}\; \vert\; g(x)\neq 0\}$}$.

Komplexe Funktionen, Fundamentalsatz der Algebra.

Analoge Begriffsbildungen gelten auch für komplexe Funktionen $ \mbox{$D\unitlength.1mm\begin{picture}(80,50) \put( 0, 0){$\longrightarrow $} \put( 10, 27){\makebox[6mm]{$\scriptstyle f$}} \end{picture} \mathbb{C}$}$ mit Definitionsbereich $ \mbox{$D\subseteq \mathbb{C}$}$, mit Ausnahme der Monotonie und der Intervalle. Eine solche Funktion heißt beschränkt genau dann, wenn für ein $ \mbox{$a\in\mathbb{R}_{> 0}$}$ stets $ \mbox{$\vert f(x)\vert\leq a$}$ ist.

Komplexe Polynome $ \mbox{$f(x) = \sum_{j = 0}^n a_j x^j$}$ haben nun die schöne Eigenschaft, laut Fundamentalsatz der Algebra in ein Produkt von Linearfaktoren

$ \mbox{$\displaystyle f(x) \; =\; (x - \omega_1)^{e_1} (x - \omega_2)^{e_2} \cdots (x - \omega_k)^{e_k} $}$
zu zerfallen, mit paarweise verschiedenen Nullstellen $ \mbox{$\omega_l\in\mathbb{C}$}$. Der Exponent $ \mbox{$e_l$}$ heißt Vielfachheit von $ \mbox{$\omega_l$}$ als Nullstelle von $ \mbox{$f$}$. Es ist $ \mbox{$\sum_{l = 1}^k e_l = n$}$.

Die Bestimmung der Nullstellen eines komplexen Polynoms kann ein verwickeltes Problem sein.

Folgen.

Ist $ \mbox{$D = \{ k\in\mathbb{Z}\; \vert \; k\geq m\}$}$ für ein $ \mbox{$m\in\mathbb{Z}$}$, so bezeichnet man eine Funktion $ \mbox{$D\unitlength.1mm\begin{picture}(80,50) \put( 0, 0){$\longrightarrow $} \put( 10, 27){\makebox[6mm]{$\scriptstyle a$}} \end{picture} \mathbb{C}$}$ als (komplexwertige) Folge, und schreibt in der Regel $ \mbox{$a(k) =: a_k$}$, sowie die gesamte Folge als $ \mbox{$a =: (a_k)_{k\geq m}$}$. Geht $ \mbox{$m$}$ aus dem Kontext hervor, so schreibt man auch $ \mbox{$a =: (a_k)_k$}$. Sind alle $ \mbox{$a_k\in\mathbb{R}$}$, so spricht man von einer reellwertigen Folge.

Eine reellwertige Folge heißt monoton wachsend, falls die zugehörige Funktion monoton wachsend ist, d.h. falls $ \mbox{$a_k \leq a_{k+1}$}$ für alle $ \mbox{$k\geq m$}$. Analog monoton fallend usf.

(Autoren: Künzer/Martin/Nebe)
[Beispiele] [Verweise]
  automatisch erstellt am 25.  1. 2006