Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Taylorentwicklung

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Satz von Taylor.

Sei $ \mbox{$f:(a,b)\longrightarrow \mathbb{R}$}$ eine reellwertige Funktion, $ \mbox{$a,b\in\hat{\mathbb{R}}$}$, $ \mbox{$a < b$}$. Sei $ \mbox{$n\geq 0$}$, und sei $ \mbox{$f$}$ als $ \mbox{$(n+1)$}$fach differenzierbar vorausgesetzt.

Seien $ \mbox{$x,x_0\in (a,b)$}$ gegeben. Es gibt ein $ \mbox{$\xi\in\mathbb{R}$}$, das zwischen $ \mbox{$x_0$}$ und $ \mbox{$x$}$ liegt, dergestalt, daß

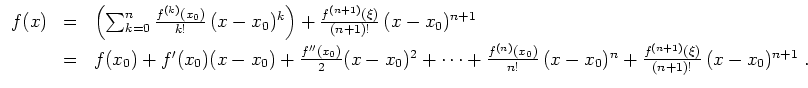
$ \mbox{$\displaystyle \begin{array}{rcl} f(x) & = & \left(\sum_{k = 0}^n \fra... ...-x_0)^n + \frac{f^{(n+1)}(\xi)}{(n+1)!}\,(x-x_0)^{n+1}\; . \\ \end{array}$}$
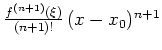Kennt man eine Abschätzung des Lagrangeschen Restgliedes $ \mbox{$\frac{f^{(n+1)}(\xi)}{(n+1)!}\,(x-x_0)^{n+1}$}$ unabhängig von $ \mbox{$\xi$}$, gegebenfalls aber noch abhängig von $ \mbox{$x$}$ und $ \mbox{$x_0$}$, so hat erhält man eine polynomiale Approximation der Funktion $ \mbox{$f(x)$}$ mit Schranken nach oben und unten.

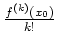Hat $ \mbox{$f(x)$}$ eine Potenzreihenentwicklung um $ \mbox{$x_0$}$, und ist $ \mbox{$x$}$ aus deren Konvergenzbereich, so stimmen die Koeffizienten $ \mbox{$\frac{f^{(k)}(x_0)}{k!}$}$ der Taylorentwicklung mit denen der Reihe überein, wie man durch $ \mbox{$k$}$-faches Differenzieren der Reihe erkennt.

Mittelwertsatz.

Setzt man $ \mbox{$n = 0$}$, so erhält man folgende Aussage.

Es gibt ein $ \mbox{$\xi$}$ zwischen $ \mbox{$x_0$}$ und $ \mbox{$x$}$ derart, daß

$ \mbox{$\displaystyle f(x) \; =\; f(x_0) + f'(\xi)(x-x_0) \; . $}$
In anderen Worten, an einer Zwischenstelle $ \mbox{$\xi$}$ stimmt die Sekantensteigung $ \mbox{$(f(x)-f(x_0))/(x-x_0)$}$ mit der Tangentensteigung $ \mbox{$f'(\xi)$}$ überein.
(Autoren: Künzer/Martin/Nebe)
[Beispiele] [Verweise]
  automatisch erstellt am 25.  1. 2006