Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Bernoulli, Riccati, Zentrische

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Bernoullische Differentialgleichung.

Eine Gleichung der Form

$ \mbox{$\displaystyle y' \;=\; a(x)y + b(x)y^\alpha $}$
mit stetigen Funktionen $ \mbox{$a(x)$}$, $ \mbox{$b(x)$}$ und $ \mbox{$\alpha\in\mathbb{R}\backslash \{0,1\}$}$ heißt Bernoullische Differentialgleichung.

Durch die Substitution $ \mbox{$u=y^{1-\alpha}$}$, $ \mbox{$u'=(1-\alpha)y^{-\alpha}y'$}$, wird daraus die lineare Gleichung

$ \mbox{$\displaystyle u' \;=\; (1-\alpha)a(x)u + (1-\alpha)b(x) \;. $}$

Riccatische Differentialgleichung.

Eine Gleichung der Form

$ \mbox{$\displaystyle y' \;=\; a(x)y^2 + b(x)y + c(x) $}$
mit stetigen Funktionen $ \mbox{$a(x)$}$, $ \mbox{$b(x)$}$, $ \mbox{$c(x)$}$ heißt Riccatische Differentialgleichung.

Für diese Gleichung kennt man kein vollständiges Lösungsverfahren.

Kennt man jedoch eine partikuläre Lösung $ \mbox{$y=\eta(x)$}$, so findet man die allgemeine Lösung durch die Substitution

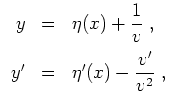
$ \mbox{$\displaystyle \begin{array}{rcl} y &=& \eta(x)+{\displaystyle\frac{1}{... ...vspace*{2mm}\\ y' &=& \eta'(x)-{\displaystyle\frac{v'}{v^2}}\;, \end{array}$}$
was uns auf die lineare Gleichung
$ \mbox{$\displaystyle v' \;=\; -(b(x)+2a(x)\eta(x))v-a(x) $}$
führt.

Die Gleichung $ \mbox{$y'=f(y/x)$}$.

Wir betrachten eine Gleichung der Form

$ \mbox{$\displaystyle y' \;=\; f(y/x) $}$
mit einer stetigen Funktion $ \mbox{$f$}$.

Im Richtungsfeld hängt die Steigung also nur von der Ursprungsgeraden ab, auf der man sich befindet.

Ist $ \mbox{$y=\eta(x)$}$ eine Lösung einer solchen Gleichung, so auch deren zentrische Streckung $ \mbox{$\tilde{\eta}(x):=\lambda\eta(x/\lambda)$}$ um den Faktor $ \mbox{$\lambda>0$}$.

Ist eine Differentialgleichung $ \mbox{$y'=g(x,y)$}$ gegeben, so kann diese genau dann auf die Form $ \mbox{$y'=f(y/x)$}$ gebracht werden, wenn $ \mbox{$g(\lambda x,\lambda y)=g(x,y)$}$ stets.

Die Substitution $ \mbox{$u=y/x$}$ führt auf die trennbare Gleichung

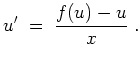
$ \mbox{$\displaystyle u' \;=\; \frac{f(u)-u}{x} \;. $}$
(Autoren: Künzer/Martin/Nebe)
[Beispiele] [Verweise]
  automatisch erstellt am 25.  1. 2006