Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Spezielle Differentialgleichungen zweiter Ordnung

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Autonome Differentialgleichung.

Eine Gleichung der Form

$ \mbox{$\displaystyle y'' \;=\; G(y,y') $}$
heißt autonome Gleichung. Dabei tritt also die unabhängige Variable $ \mbox{$x$}$ nicht explizit auf.

Der Ansatz

$ \mbox{$\displaystyle y' \;=\; v(y) $}$
mit einer zu bestimmenden Funktion $ \mbox{$v$}$ führt auf
$ \mbox{$\displaystyle y''   \;=\; v'(y)y' \;=\; v'(y)v(y) $}$
und somit auf die Gleichung erster Ordnung
$ \mbox{$\displaystyle v' \;=\; G(y,v)/v \; . $}$
Diese ist nach $ \mbox{$v$}$ als Funktion von $ \mbox{$y$}$ aufzulösen.

Kennt man eine Lösung für $ \mbox{$v$}$, so ist $ \mbox{$y$}$ aus der trennbaren Gleichung $ \mbox{$y'=v(y)$}$ zu bestimmen.

Potenzreihenansatz.

In manchen Fällen kann eine Differentialgleichung gelöst werden unter der Annahme, daß die Lösung $ \mbox{$y$}$ eine Potenzreihenentwicklung

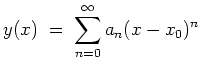
$ \mbox{$\displaystyle y(x) \;=\; \sum_{n=0}^\infty a_n (x-x_0)^n $}$
besitzt.

Es gilt dann

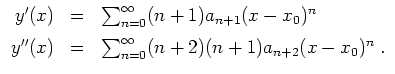
$ \mbox{$\displaystyle \begin{array}{rcl} y'(x) &=& \displaystly\sum_{n=0}^{\in... ...=& \displaystly\sum_{n=0}^{\infty} (n+2)(n+1)a_{n+2}(x-x_0)^n \;. \end{array}$}$

Setzt man dies in eine Differentialgleichung $ \mbox{$F(x,y,y',y'')=0$}$ ein und ordnet nach Potenzen von $ \mbox{$x-x_0$}$, so erhält man ein unendliches Gleichungssystem für die Koeffizienten $ \mbox{$a_n$}$. In günstigen Fällen kann man für die Koeffizienten so eine Rekursionsgleichung herleiten, und manchmal auch eine geschlossene Formel.

Lineare Differentialgleichung zweiter Ordnung mit konstanten Koeffizienten, homogener Fall.

Wir betrachten eine Gleichung der Form

$ \mbox{$\displaystyle y''+ay'+by \;=\; 0 $}$
mit Konstanten $ \mbox{$a,b\in\mathbb{R}$}$.

Der Ansatz $ \mbox{$y = e^{\lambda x}$}$ führt auf

$ \mbox{$\displaystyle y''+ay'+by \;=\; e^{\lambda x}(\lambda^2 + a\lambda + b) \; =\; 0\; . $}$
Das Polynom $ \mbox{$p(\lambda)=\lambda^2+a\lambda+b$}$ heißt charakteristisches Polynom der Gleichung. Es seien $ \mbox{$\lambda_1,\lambda_2\in\mathbb{C}$}$ die beiden (eventuell identischen) Nullstellen von $ \mbox{$p(\lambda)$}$.

Dann ist wegen des linearen Charakters der Gleichung die Funktion

$ \mbox{$\displaystyle y \; =\; c_1 e^{\lambda_1 x} + c_2 e^{\lambda_2 x} $}$
eine Lösung für $ \mbox{$c_1,\, c_2\,\in\,\mathbb{R}$}$. Sind $ \mbox{$\lambda_1$}$ und $ \mbox{$\lambda_2$}$ reell und verschieden, so ist dies die allgemeine Lösung.

Sind $ \mbox{$\lambda_1 = \alpha + \mathrm{i}\beta$}$ und $ \mbox{$\lambda_2 = \alpha - \mathrm{i}\beta$}$ komplex und verschieden, so verwendet man für die allgemeine reelle Lösung den Real- und den Imaginärteil von $ \mbox{$e^{\lambda_1 x}$}$, und wir erhalten

$ \mbox{$\displaystyle y \; =\; c_1 e^{\alpha x} \cos(\beta x) + c_2 e^{\alpha x} \sin(\beta x) $}$
für $ \mbox{$c_1,\, c_2\,\in\,\mathbb{R}$}$ als allgemeine Lösung.

Bleibt der Fall einer doppelten reellen Nullstelle $ \mbox{$\lambda_1 = \lambda_2$}$ des charakteristischen Polynoms zu betrachten. Um auch hier zu einer zweiten Grundlösung zu kommen, variieren wir die Konstante $ \mbox{$c_1$}$, setzen also $ \mbox{$y = c_1(x)\, e^{\lambda_1 x}$}$ an, und erhalten wegen $ \mbox{$a = -2\lambda_1$}$

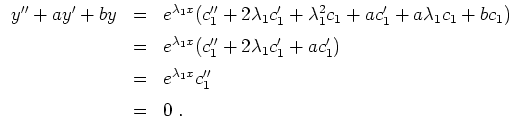
$ \mbox{$\displaystyle \begin{array}{rcl} y''+ay'+by &=& e^{\lambda_1 x}(c_1''... ...} \\ &=& e^{\lambda_1 x} c_1''\vspace*{2mm} \\ &=& 0\; . \\ \end{array}$}$
Eine Lösung für $ \mbox{$c_1$}$ ist gegeben durch $ \mbox{$c_1 = x$}$. Damit ergibt sich als weitere Lösung $ \mbox{$y = x e^{\lambda_1 x}$}$, und allgemeine Lösung lautet
$ \mbox{$\displaystyle y = (c_1 + c_2 x)e^{\lambda_1 x} $}$
mit $ \mbox{$c_1,\, c_2\,\in\,\mathbb{R}$}$.

Lineare Differentialgleichung zweiter Ordnung mit konstanten Koeffizienten, allgemeiner Fall.

Wir betrachten eine Gleichung der Form

$ \mbox{$\displaystyle y''+ay'+by \;=\; f(x) $}$
mit Konstanten $ \mbox{$a,b\in\mathbb{R}$}$ und einer stetigen Funktion $ \mbox{$f$}$. Die allgemeine Lösung der zugehörigen homogenen Gleichung sei bekannt und von der Form $ \mbox{$y=c_1y_1(x)+c_2y_2(x)$}$ mit zwei Grundlösungen $ \mbox{$y_1, y_2$}$.

Um eine partikuläre Lösung der allgemeinen Gleichung zu finden, variieren wir die Konstanten. Dies ergibt den Ansatz

$ \mbox{$\displaystyle y \;=\; c_1(x)y_1(x)+c_2(x)y_2(x) $}$
und führt auf die Gleichung
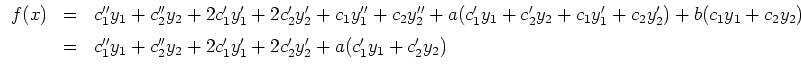
$ \mbox{$\displaystyle \begin{array}{rcl} f(x) &=& c_1''y_1+c_2''y_2+2c_1'y_1'+... ... &=& c_1''y_1+c_2''y_2+2c_1'y_1'+2c_2'y_2'+ a(c_1'y_1+c_2'y_2) \end{array}$}$
Diese Gleichung kann vereinfacht werden durch die zusätzliche, willkürliche Bedingung
$ \mbox{$\displaystyle (\ast) \rule{4cm}{0cm} c_1'y_1+c_2'y_2 \;=\; 0 \;, \rule{4cm}{0cm} $}$
welche abgeleitet
$ \mbox{$\displaystyle c_1''y_1+c_2''y_2+c_1'y_1'+c_2'y_2' \;=\; 0 $}$
ergibt. Es bleibt also die Gleichung
$ \mbox{$\displaystyle f(x) \;=\; c_1'y_1'+c_2'y_2' $}$
zusammen mit $ \mbox{$(\ast)$}$ zu erfüllen. Diese beiden Gleichungen lassen sich nach $ \mbox{$c_1'$}$ und $ \mbox{$c_2'$}$ auflösen. Mit der Wronski-Determinante $ \mbox{$W(x):=y_1(x)y_2'(x)-y_2(x)y_1'(x)$}$ folgt
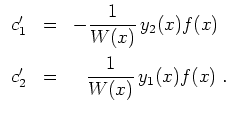
$ \mbox{$\displaystyle \begin{array}{rcr} c_1' & = & -{\displaystyle\frac{1}{W(... ...2mm}\\ c_2' & = & {\displaystyle\frac{1}{W(x)}}\,y_1(x)f(x) \;. \end{array}$}$
In günstigen Fällen lassen sich $ \mbox{$c_1(x)$}$ und $ \mbox{$c_2(x)$}$ hieraus bestimmen. Die allgemeine Lösung der Gleichung
$ \mbox{$\displaystyle y''+ay'+by \;=\; f(x) $}$
lautet dann
$ \mbox{$\displaystyle y \;=\; (C_1y_1(x)+C_2y_2(x))+(c_1(x)y_1(x)+c_2(x)y_2(x)) \;. $}$
mit beliebigen Konstanten $ \mbox{$C_1,C_2\in\mathbb{R}$}$.
(Autoren: Künzer/Martin/Nebe)

Beispiele:

[Verweise]
  automatisch erstellt am 25.  1. 2006