Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] Englische Flagge
Mathematik-Online-Lexikon:

Parameterintegrale und iterierte Integrale

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Sei $ f = f(x_1, \ldots , x_n)$ eine stetige reelle skalare Funktion. Ein Integral der Form

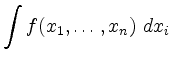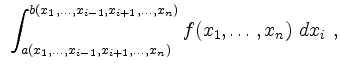
$\displaystyle \int f(x_1, \ldots , x_n) \ dx_i \ $   oder$\displaystyle \ \int_{a(x_1, \ldots ,x_{i-1}, x_{i+1}, \ldots ,x_n)}^{b(x_1, \ldots ,x_{i-1}, x_{i+1}, \ldots ,x_n)} f(x_1, \ldots , x_n) \ dx_i \ ,$

in dem alle Variablen $ x_j$ mit $ j \neq i$ als Konstanten ( festgewählte Parameter genannt) betrachtet werden, nennt man Parameterintegral. Man kann solche Integrale als Umkehroperation zur partiellen Ableitung nach $ x_i$ betrachten.

Unter einem iterierten Integral versteht man eine Iteration von Parameterintegralen der Gestalt

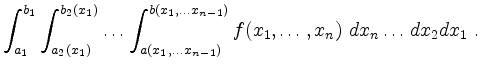
$\displaystyle \int_{a_1}^{b_1} \int_{a_2(x_1)}^{b_2(x_1)} \ldots \int_{a(x_1,... ...})}^{b(x_1, \ldots x_{n-1})} f(x_1, \ldots , x_n) \ dx_n \ldots dx_2 dx_1 \ .$

Die Auswertung erfolgt von innen nach außen. Für jede Anordnung der Variablen läßt sich analog ein iteriertes Integral definieren.

siehe auch:

  automatisch erstellt am 27.  5. 2008