Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Nichtlineares Gleichungssystem

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Ein nichtlineares Gleichungssystem hat die Form

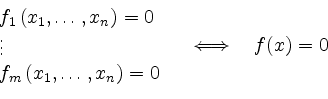
\begin{displaymath} \begin{array}{l} f_1\left(x_1,\ldots ,x_n \right)=0 \\ \vdo... ...\right)=0 \end{array} \quad \Longleftrightarrow \quad f(x)=0 \end{displaymath}

mit Unbekannten $ x_j$ und gegebenen Funktionen $ f_j$ .

Im Gegensatz zu linearen Gleichungssystemen können keine generellen Aussagen über die Lösbarkeit gemacht werden. Im Allgemeinen existieren jedoch für $ m=n$ nur endlich viele Lösungen.

Für $ m>n$ ist das System normalerweise überbestimmt. Es existiert keine Lösung und man spricht von einem nichtlinearen Ausgleichsproblem. Für $ m<n$ ist das System im Allgemeinen unterbestimmt, d.h. Unbekannte $ x_j$ können frei gewählt werden.

Beispiel:

[Verweise]
  automatisch erstellt am 19.  8. 2013