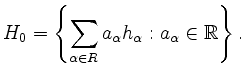Für
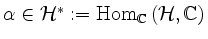 setze
setze
Eine Linearform
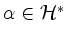 heißt Wurzel von
heißt Wurzel von  bzgl.
bzgl. 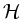 , falls
, falls
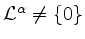 und
und
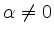 ist.
ist.
Die Menge der Wurzeln, genannt Wurzelsystem, wird mit
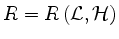 bezeichnet.
bezeichnet.
Es gelten folgende Aussagen:
-
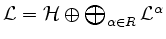
-
![$ \left[{\cal L}^\alpha,{\cal L}^\beta\right]\subseteq{\cal L}^{\alpha+\beta}$](/inhalt/aussage/aussage1381/img10.png) für
für 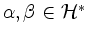
-
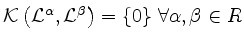 mit
mit 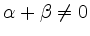
- Die Restriktion von
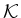 auf
auf
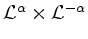 ist für jedes
ist für jedes
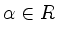 nicht-ausgeartet, ebenso die Restriktion auf
nicht-ausgeartet, ebenso die Restriktion auf 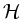 .
.
- Für alle
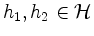 gilt
gilt
- Für alle
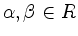 und alle
und alle
![$ h\in\left[{\cal L}^\alpha,{\cal L}^{-\alpha}\right]$](/inhalt/aussage/aussage1381/img20.png) gibt es ein
gibt es ein
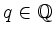 so, dass
so, dass
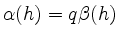 ist.
ist.
- Zu jedem
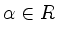 und zu jedem
und zu jedem
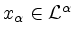 gibt es
gibt es
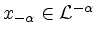 und
und
![$ h_\alpha\in\left[{\cal L}^\alpha,{\cal L}^{-\alpha}\right]$](/inhalt/aussage/aussage1381/img25.png) so, dass
so, dass
![$ \left[h_\alpha,x_\alpha\right]=2x_\alpha,~\left[h_\alpha,x_{-\alpha}\right]=-2x_{-\alpha},~\left[x_\alpha,x_{-\alpha}\right]=h_{\alpha}$](/inhalt/aussage/aussage1381/img26.png) gilt.
gilt.
-
![$ \operatorname{dim}({\cal L}^\alpha)=\operatorname{dim}\left[{\cal L}^\alpha,{\cal L}^{-\alpha}\right]=1~\forall\alpha\in R$](/inhalt/aussage/aussage1381/img27.png) .
.
Desweiteren gilt:
Ist 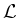 eine komplexe, halbeinfache Lie-Algebra,
eine komplexe, halbeinfache Lie-Algebra, 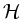 eine Cartansche Teilalgebra von
eine Cartansche Teilalgebra von 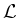 ,
, 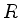 das zugehörige Wurzelsystem und
das zugehörige Wurzelsystem und
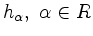 , wie oben, dann gilt:
, wie oben, dann gilt:
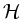 wird aufgespannt von
wird aufgespannt von
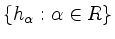
-
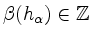 für alle
für alle
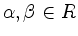
-
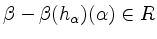 für alle
für alle
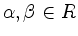
- Für alle
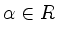 und
und
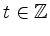 gilt
gilt
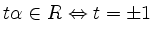
Es bezeichne 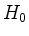 der von
der von
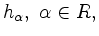 aufgespannte
aufgespannte
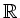 -Vektorraum, also
-Vektorraum, also
Nach Obigem gilt
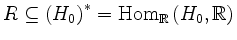 ,
,
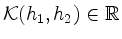 und
und
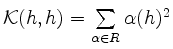 für alle
für alle
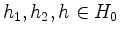 . Also ist die Restriktion der Killing-Form auf
. Also ist die Restriktion der Killing-Form auf 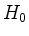 positiv definit.
positiv definit.
Mit Hilfe des
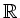 -Vektorraum-Isomorphismus
-Vektorraum-Isomorphismus
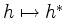 ,
,
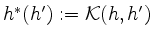 von
von 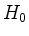 auf
auf 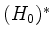 erhalten wir eine positiv-definite, symmetrische Bilinearform auf
erhalten wir eine positiv-definite, symmetrische Bilinearform auf 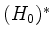 , definiert durch
, definiert durch
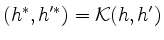
für
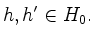
Damit wird das Wurzelsystem
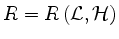 zu einer Teilmenge eines euklidischen Vektorraumes.
zu einer Teilmenge eines euklidischen Vektorraumes.
Für alle
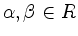 ,
, 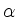 nicht proportional zu
nicht proportional zu 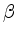 , gibt es
, gibt es
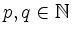 so, dass gilt:
so, dass gilt:
-
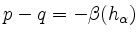
-
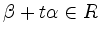 für
für
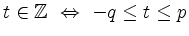
(Autor: Hablizel)
| |
automatisch erstellt
am 8. 3. 2007 |


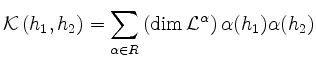
![]() eine komplexe, halbeinfache Lie-Algebra,
eine komplexe, halbeinfache Lie-Algebra, ![]() eine Cartansche Teilalgebra von
eine Cartansche Teilalgebra von ![]() ,
, ![]() das zugehörige Wurzelsystem und
das zugehörige Wurzelsystem und
![]() , wie oben, dann gilt:
, wie oben, dann gilt: