Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Zusammenhang zwischen zweikantengefärbeten Graphen und den Teilmengen von endlichen Mengen

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht
Die Menge $ K \subseteq \{1,\dots, n\}$ wird bijektiv auf einen Teilgraphen des folgenden zweikantengefärbten Graphen $ G(n)$ abgebildet.

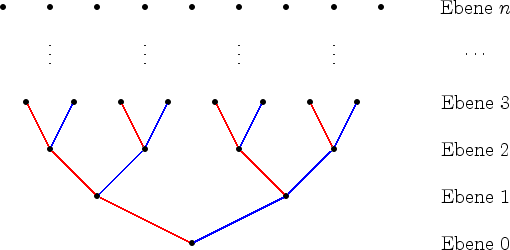
\includegraphics{zweikanten_graph1}

Das Bild von $ K$ in $ G(n)$ wird folgendermaßen konstruiert:
Man durchläuft den Graphen $ G(n)$ von unten nach oben bis zur Ebene $ n$. Beim Schritt von der Ebene $ i-1$ zur Ebene $ i$ wählt man eine blaue Kante, falls $ i \in K$ gilt, anderenfalls eine rote. Auf diese Weise erhält man z.B. für $ n=3$ und $ K = \{1,3\}$ in $ G(3)$ den Weg:

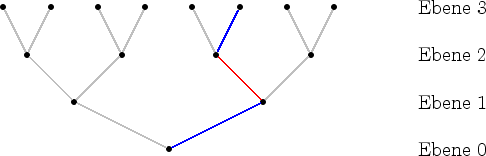
\includegraphics{zweikanten_graph2}

Mit Hilfe dieser Abbildung lässt sich zeigen:

Die Anzahl der $ k$-elementigen Teilmenge einer Menge mit $ n$ Elementen ist

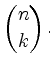
$\displaystyle \displaystyle \binom{n}{k}\,.$

(Aus: Vorkurs Mathematik)

siehe auch:

[Erläuterungen]
  automatisch erstellt am 26.  2. 2007