Der Simplex-Algorithmus zur Lösung eines linearen
Programms
modifiziert eine zulässige Basislösung  mit
sukzessiven Pivot-Operationen, bis ein optimaler
Vektor
mit
sukzessiven Pivot-Operationen, bis ein optimaler
Vektor
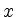 erreicht ist.
Ein Schritt
der das Simplex-Tableau
erreicht ist.
Ein Schritt
der das Simplex-Tableau
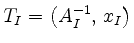 verwendet, hat die folgende Form:
verwendet, hat die folgende Form:
(i) Zuerst berechnet man mit 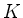 , der
Komplementärmenge von
, der
Komplementärmenge von 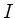 ,
,
und definiert 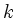 als den kleinsten Index, an dem
als den kleinsten Index, an dem
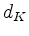 sein Minimum annimmt.
Falls
sein Minimum annimmt.
Falls
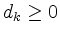 , ist die aktuelle Basislösung
, ist die aktuelle Basislösung  optimal und der Algorithmus bricht ab.
optimal und der Algorithmus bricht ab.
(ii) Ist der Hilfsvektor
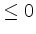 , so
ist das Infimum der Zielfunktion
, so
ist das Infimum der Zielfunktion 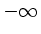 ,
und das lineare Programm hat keine Lösung.
Andernfalls wählt man
,
und das lineare Programm hat keine Lösung.
Andernfalls wählt man 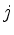 als den kleinsten Index,
für den der Quotient
minimal ist.
als den kleinsten Index,
für den der Quotient
minimal ist.
(iii) Das Tableau 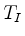 wird aktualisiert,
wird aktualisiert,
indem man
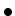
- die Zeile mit Index
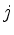 durch
durch 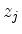 dividiert,
dividiert,
und
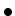
- für jedes
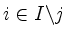 von der Zeile mit Index
von der Zeile mit Index 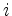 die modifizierte
Zeile mit Index
die modifizierte
Zeile mit Index 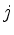 , multipliziert mit
, multipliziert mit
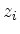 , subtrahiert.
, subtrahiert.
Beispiel:
| |
automatisch erstellt
am 19. 8. 2013 |




![]() , der
Komplementärmenge von
, der
Komplementärmenge von ![]() ,
,
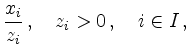
![]() wird aktualisiert,
wird aktualisiert,