Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Bernoulli-Polynome

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Die normalisierten Bernoulli-Polynome sind durch die Rekursion

$\displaystyle p_{i+1}^\prime = p_i,\quad p_0(x)=1 $

definiert, wobei $ \int_0^1 p_i=0$ für $ i>0$.

% begin\{minipage\} \begin{minipage}[t]{0.56\linewidth} \mbox{} \begin{center... ...c{1}{24} x^2 - \frac{1}{720} \end{array} \end{displaymath} \end{minipage}


Die normalisierten Bernoulli-Polynome sind symmetrisch bezüglich $ t=1/2$, d.h. $ p_{2i-1}(\cdot-1/2)$ und $ p_{2i}(\cdot-1/2)$ sind ungerade bzw. gerade Funktionen.

Weiter gilt

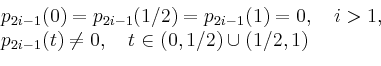
\begin{displaymath} \begin{array}{l} p_{2i-1}(0) = p_{2i-1}(1/2) = p_{2i-1}(1)... ... p_{2i-1}(t) \ne 0,\quad t\in(0,1/2)\cup(1/2,1) \end{array} \end{displaymath}

und

$\displaystyle \gamma_{2i} = p_{2i}(0) = p_{2i}(1) $

ist entweder ein Minimum oder Maximum von $ p_{2i}$ auf $ [0,1]$.

Die Werte $ \gamma_{2i}$ werden als normierte Bernoulli-Zahlen bezeichnet. Für $ 2i \leq 16$ sind sie in der folgenden Tabelle angegeben.

\begin{displaymath} \renewedcommand{arraystretch}{1.5} \begin{array}{\vert c\v... ...000} \\ \hline \end{array} \renewedcommand{arraystretch}{1} \end{displaymath}

Erläuterung:

[Verweise]
  automatisch erstellt am 19.  8. 2013