Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] Englische Flagge
Mathematik-Online-Lexikon:

Steilster Abstieg

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Die Methode des steilsten Abstiegs dient zur Minimierung multivariater Funktionen $ f(x_1,\ldots,x_n)$. Zur Durchführung eines Iterationsschrittes $ x\to y$ wird zunächst der negative Gradient

$\displaystyle d = -\operatorname{grad}f(x) $

als lokal beste Abstiegsrichtung berechnet. Dann wird $ y$ als eine Minimalstelle von $ f$ in Richtung von $ d$ bestimmt:

$\displaystyle f(y) = \min_{t\ge 0} f(x+td) \,. $

\includegraphics[width=0.55\linewidth]{Bild_Steilster_Abstieg_Aussage}

Wie in der Abbildung illustriert, ist die Suchrichtung orthogonal zu der Niveaumenge durch $ x$ und berührt eine Niveaumenge zu einem kleineren Funktionswert in $ y$.

Die Konvergenz der durch die Methode des steilsten Abstiegs erzeugten Folge $ x_0,x_1,\ldots$ kann unter sehr allgemeinen Voraussetzungen gezeigt werden. Hinreichend ist, dass $ f$ nach unten beschränkt ist und $ \operatorname{grad}f$ in einer Umgebung $ U$ der Menge $ \{x: f(x) \leq f(x_0)\}$ Lipschitz-stetig ist, d.h.

$\displaystyle \Vert \operatorname{grad}f(x) - \operatorname{grad}f(\tilde x) \Vert \le L \Vert x-\tilde x\Vert,\quad x,\tilde x\in U \,. $

Dann gilt

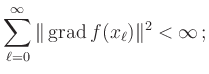
$\displaystyle \sum_{\ell=0}^\infty \Vert\operatorname{grad}f(x_\ell)\Vert^2 < \infty \,; $

insbesondere ist $ \Vert\operatorname{grad}f(x_\ell)\Vert$ eine Nullfolge.

Dies impliziert insbesondere, dass jeder Häufungspunkt der Folge $ x_0,x_1,\ldots$ ein kritischer Punkt von $ f$ ist. Dass es sich um ein lokales Minimum handelt ist statistisch gesehen fast sicher, kann jedoch nicht zwingend gefolgert werden.

In dem Algorithmus braucht die eindimensionale Minimierung nur näherungsweise durchgeführt werden. Die Suchrichtung $ d$ muss nicht als der negative Gradient gewählt, und eine globale Minimalstelle $ y$ nicht bestimmt werden. Entscheidend für die Konvergenz ist lediglich, dass in jedem Iterationsschritt eine Reduktion des Funktionswertes proportional zu $ \Vert\operatorname{grad}f(x)\Vert^2$ erreicht wird.

siehe auch:

[Downloads] [Beispiele]
  automatisch erstellt am 14.  6. 2016