Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Lineares Mehrschrittverfahren

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Ein lineares $ n$ -Schrittverfahren mit Parametern $ a_k$ und $ b_k$ zur Approximation der Lösung $ (u_1(t),\ldots,u_d(t))^t$ eines Differentialgleichungssystems

$\displaystyle u^\prime = f(t,u),\quad $

hat die Form

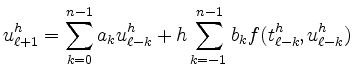
$\displaystyle u^h_{\ell+1} = \sum_{k=0}^{n-1} a_k u^h_{\ell-k} + h \sum_{k=-1}^{n-1} b_k f(t^h_{\ell-k},u^h_{\ell-k}) $

mit $ t^h_\ell = t_0 + \ell h$ und $ u^h_\ell$ der Approximation von $ u(t^h_\ell)$ .


\includegraphics[width=0.6\linewidth]{Bild_Mehrschrittverfahren.eps}

Wie in der Abbildung illustriert ist, basiert ein Schritt des Verfahrens auf den $ n$ zuletzt berechneten Approximationen. Zum Starten eines Mehrschrittverfahrens ist deshalb eine zusätzliche Prozedur erforderlich. Die ersten $ n$ Approximationen $ u^h_0,\ldots,u^h_{n-1}$ können beispielsweise durch Taylor-Entwicklung oder mit Hilfe eines Einschrittverfahrens ausgehend von dem Anfangswert $ u(t_0)$ berechnet werden.

Man unterscheidet zwischen expliziten und impliziten Mehrschrittverfahren, jenachdem ob der Koeffizient $ b_{-1}$ von $ u^h_{\ell+1}$ Null oder ungleich Null ist. Explizite Mehrschrittverfahren benötigen nur eine Auswertung der Funktion $ f$ pro Schritt. Sie sind deshalb sehr effizient. Implizite Verfahren sind zwar etwas aufwändiger zur implementieren, haben jedoch im allgemeinen bessere Stabilitätseigenschaften.

siehe auch:

[Beispiele]
  automatisch erstellt am 19.  8. 2013