Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Adams-Moulton-Verfahren

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Das Adams-Moulton-Verfahren zur Approximation des Differentialgleichungssystems

$\displaystyle u^\prime = f(t,u) $

ist eine implizite Variante des Adams-Bashforth-Verfahrens. Es basiert ebenfalls auf der Identität

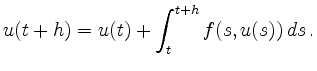
$\displaystyle u(t+h) = u(t) + \int_{t}^{t+h} f(s,u(s))\,ds \,. $

Man approximiert den Integrand durch ein (vektorwertiges) Polynom $ p$ vom Grad $ <n$, das an den Punkte $ s=t^h_{\ell+1},\ldots,t^h_{\ell-n+1}$ ( $ t^h_\ell = t_0 + \ell h$) interpoliert. Zusätzlich zu den beim Adams-Bashforth-Verfahren verwendeten Daten wird der noch unbekannte Wert $ u^h_{\ell+1}$ in die in die Interpolation mit einbezogen.

Mit der Lagrange-Darstellung von $ p$ erhält man ein $ n$-Schrittverfahren der Ordnung $ n+1$:

$\displaystyle u^h_{\ell+1} = u^h_\ell + h \sum_{k=-1}^{n-1} b_k f(t^h_{\ell-k},u^h_{\ell-k}) $

mit

$\displaystyle b_k = \int_0^1 \prod_{j=-1,j\ne k}^{n-1} \frac{s+j}{j-k}\,ds \,. $

Die Koeffizienten der Verfahren bis zur Ordnung $ n=6$ sind in der folgenden Tabelle angegeben.

$ n$ $ b_{-1}$ $ b_0$ $ b_1$ $ b_2$ $ b_3$ $ b_4$ $ b_5$
$ 1$ $ \frac{1}{2}$ $ \frac{1}{2}$          
$ 2$ $ \frac{5}{12}$ $ \frac{8}{12}$ $ -\frac{1}{12}$        
$ 3$ $ \frac{9}{24}$ $ \frac{19}{24}$ $ -\frac{5}{24}$ $ \frac{1}{24}$      
$ 4$ $ \frac{251}{720}$ $ \frac{646}{720}$ $ -\frac{264}{720}$ $ \frac{106}{720}$ $ -\frac{19}{720}$    
$ 5$ $ \frac{475}{1440}$ $ \frac{1427}{1440}$ $ -\frac{798}{1440}$ $ \frac{482}{1440}$ $ -\frac{173}{1440}$ $ \frac{27}{1440}$  
$ 6$ $ \frac{19087}{60480}$ $ \frac{65112}{60480}$ $ -\frac{46461}{60480}$ $ \frac{37504}{60480}$ $ -\frac{20211}{60480}$ $ \frac{6312}{60480}$ $ -\frac{863}{60480}$

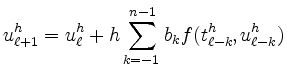
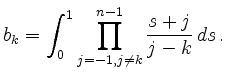
Da beim Adams-Moulton-Verfahren in jedem Schritt ein nichtlineares Gleichungssystem zur Bestimmung von $ u^h_{\ell+1}$ gelöst werden muss, wird das Verfahren üblicherweise in Verbindung mit einem expliziten Mehrschrittverfahren zur Schätzung des gesuchten Wertes verwendet. Der Mehraufwand wird im allgemeinen durch bessere Stabilitätseigenschaften kompensiert.

Erläuterung:

[Verweise]
  automatisch erstellt am 19.  8. 2013