Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Konvexe Funktion

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht
Eine Funktion ist (strikt) konvex auf einem Intervall D, wenn jede Sekante (echt) oberhalb des Graphen liegt, d.h.

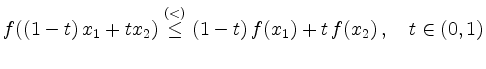
$\displaystyle f((1-t)\,x_1+tx_2) \stackrel{(<)}{\leq} (1-t)\,f(x_1)+t\,f(x_2)\,,\quad t \in (0,1) $

für alle $ x_i \in D$ .

\includegraphics[width=.7\linewidth]{konvexe_funktion}

Ist $ f$ zweimal stückweise stetig differenzierbar, so ist (strikte) Konvexität äquivalent zu

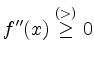
$\displaystyle f''(x) \stackrel{(>)}{\geq} 0 $

für alle $ x \in D$ bis auf isolierte Punkte.

Die Summe konvexer Funktionen ist konvex. Die Operationen $ -,\cdot,/$ sowie die Hintereinanderschaltung $ \circ$ erhalten die Konvexität im allgemeinen nicht. Schließlich ist jede konvexe Funktion stetig.

Analog definiert man konkav. Für eine konkave Funktion liegen die Sekanten unterhalb des Graphen, d.h. die an der $ x$ -Achse gespiegelte Funktion $ -f$ ist konvex.

Erläuterung:

[Verweise]
  automatisch erstellt am 19.  8. 2013