Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Müllers Verfahren

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Mit Müllers Verfahren können sowohl reelle als auch komplexe Nullstellen einer Funktion $ f$ approximiert werden. Dabei wird eine Folge $ z_0,z_1,\ldots$ von Näherungen für eine Nullstelle $ z_*$ mit Hilfe von quadratischer Interpolation generiert. Die Approximation $ z_{\ell+1}$ ist die am nächsten bei $ z_\ell$ gelegene Nullstelle der Parabel, die die Punkte

$\displaystyle (z_k,f(z_k)),\quad k=\ell,\ell-1,\ell-2 \,, $

interpoliert:

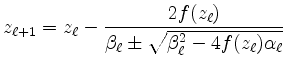
$\displaystyle z_{\ell+1} = z_\ell -\frac{2f(z_\ell)}{ \beta_\ell \pm \sqrt{\beta_\ell^2 - 4 f(z_\ell)\alpha_\ell}} $

mit

$\displaystyle \alpha_\ell = \Delta(z_\ell,z_{\ell-1},z_{\ell-2})f, \quad \beta_\ell = \Delta(z_\ell,z_{\ell-1})f + \alpha_\ell(z_\ell-z_{\ell-1}) $

und dem Vorzeichen so gewählt, dass der Betrag des Nenners am größten wird.

Im Fall von zusammenfallenden Punkten sind die Dividierten Differenzen mit Hilfe entsprechender Ableitungen definiert. Allerdings steht dies nicht im Einklang mit dem ableitungsfreien Charakter des Verfahrens. In der Praxis treten jedoch solche und andere Ausnahmefälle ( $ \alpha_\ell=0$ , $ z_{\ell+1}= \infty$ ) sehr selten auf.

Für glatte Funktionen konvergiert Müllers Verfahren lokal fast mit Ordnung $ 2$ .

Erläuterung:

[Beispiele] [Verweise]
  automatisch erstellt am 19.  8. 2013