Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Cauchysche Integralformel

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Die Cauchysche Integralformel ermöglicht es, grob gesprochen, von der Kenntnis einer holomorphen Funktion auf dem Rand eines Gebietes auf einen Funktionswert (resp. auf die Werte der höheren Ableitungen) im Innern zu schließen. Sei dazu $ \mbox{$G\subseteq \mathbb{C}$}$ ein einfach zusammenhängendes Gebiet (`ohne Löcher'), $ \mbox{$f:G\longrightarrow \mathbb{C}$}$ eine holomorphe Funktion, sei $ \mbox{$[a,b]\subseteq \mathbb{R}$}$ und sei $ \mbox{$\gamma:[a,b]\longrightarrow G$}$ ein einfach geschlossener Integrationsweg, insbesondere sei also $ \mbox{$\gamma(a) = \gamma(b)$}$. Sei ferner $ \mbox{$z_0$}$ ein Punkt im Innern des von $ \mbox{$\gamma$}$ berandeten Gebietes.

Es gilt die Cauchysche Integralformel

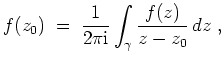
$ \mbox{$\displaystyle f(z_0)\; =\; \frac{1}{2\pi \mathrm{i}}\int_\gamma \frac{f(z)}{z-z_0}\, dz\; , $}$
und allgemeiner, für $ \mbox{$k\geq 0$}$,
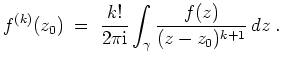
$ \mbox{$\displaystyle f^{(k)}(z_0)\; =\; \frac{k!}{2\pi \mathrm{i}}\int_\gamma \frac{f(z)}{(z-z_0)^{k+1}}\, dz\; . $}$
(Autoren: Künzer/Meister/Nebe)

siehe auch:

[Beispiele]
  automatisch erstellt am 25.  1. 2006