

Mathematik-Online-Lexikon:

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |

|
|
Mathematik-Online-Lexikon: | ||
Endliche Körper | ||
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z | Übersicht |
Codierungstheorie bedient sich der Linearen Algebra über endlichen Körpern.
Ringe und Körper
Ein Ring ist eine Menge
![]() , zusammen mit Operationen
, zusammen mit Operationen
![]() und
und
![]() , welche Assoziativ-, Kommutativ- und
Distibutivgesetze erfüllen. Ferner hat ein Ring eine
, welche Assoziativ-, Kommutativ- und
Distibutivgesetze erfüllen. Ferner hat ein Ring eine
![]() und eine
und eine
![]() , und zu jedem
, und zu jedem
![]() gibt es ein
gibt es ein
![]() mit
mit
![]() .
.
Hat jedes Element
![]() auch ein multiplikativ Inverses
auch ein multiplikativ Inverses
![]() , gilt also
, gilt also
![]() ,
so heißt
,
so heißt
![]() ein Körper.
ein Körper.
Zum Beispiel bilden die ganzen Zahlen
![]() einen Ring, aber keinen Körper. Beispiele für Körper sind
die rationalen Zahlen
einen Ring, aber keinen Körper. Beispiele für Körper sind
die rationalen Zahlen
![]() , die reellen Zahlen
, die reellen Zahlen
![]() und die komplexen Zahlen
und die komplexen Zahlen
![]() .
.
Ist
![]() ein Ring, so bezeichnet
ein Ring, so bezeichnet
![]() den Polynomring über
den Polynomring über
![]() in der Unbestimmten
in der Unbestimmten
![]() . Seine
Elemente sind Polynome mit Koeffizienten in
. Seine
Elemente sind Polynome mit Koeffizienten in
![]() , Addition und die Multiplikation sind die für
Polynome gebräuchlichen.
, Addition und die Multiplikation sind die für
Polynome gebräuchlichen.
Vorsicht, ein Polynom ist ein formaler Ausdruck, der erst durch Einsetzen von Werten für
![]() eine Funktion von
eine Funktion von
![]() nach
nach
![]() definiert. Für gewisse Grundringe
definiert. Für gewisse Grundringe
![]() ist es möglich, daß zwei verschiedene Polynome auf diese Weise
dieselbe Funktion definieren.
ist es möglich, daß zwei verschiedene Polynome auf diese Weise
dieselbe Funktion definieren.
Ein Ideal
![]() in einem Ring
in einem Ring
![]() ist eine Teilmenge, die folgende Eigenschaften erfüllt.
ist eine Teilmenge, die folgende Eigenschaften erfüllt.
Jedes Ideal
![]() in
in
![]() definiert nun einen neuen Ring, den Restklassenring
definiert nun einen neuen Ring, den Restklassenring
![]() . Formal sind dessen
Elemente Äquivalenzklassen von Elementen aus
. Formal sind dessen
Elemente Äquivalenzklassen von Elementen aus
![]() , wobei
, wobei
![]() falls
falls
![]() . Addition und Multiplikation
sind repräsentantenweise definiert.
. Addition und Multiplikation
sind repräsentantenweise definiert.
In der Praxis rechnet man in
![]() mit den Elementen aus
mit den Elementen aus
![]() , nur unter Berücksichtigung der Tatsache, daß die
Elemente in
, nur unter Berücksichtigung der Tatsache, daß die
Elemente in
![]() alle verschwinden. Insbesondere kann man während einer Rechnung die einzelnen Terme beliebig
modulo
alle verschwinden. Insbesondere kann man während einer Rechnung die einzelnen Terme beliebig
modulo
![]() abändern. Von der Äquivalenzklassendefinition merke man sich in erster Linie, daß auf diese
Weise die Zahl der Elemente von
abändern. Von der Äquivalenzklassendefinition merke man sich in erster Linie, daß auf diese
Weise die Zahl der Elemente von
![]() als Zahl der Äquivalenzklassen in
als Zahl der Äquivalenzklassen in
![]() ermittelt werden kann.
ermittelt werden kann.
Zum Beispiel hat
![]() die Elemente
die Elemente
![]() und
und
![]() .
Es wird in
.
Es wird in
![]() repräsentantenweise
repräsentantenweise
Endliche Körper
Wir definieren nun zunächst die endlichen Primkörper als
![]() für alle Primzahlen
für alle Primzahlen
![]() .
.
Ein Polynom
![]() in
in
![]() heißt irreduzibel, falls es sich nicht
als Produkt zweier Polynome von echt kleinerem Grad schreiben läßt. Das läßt sich in der Praxis oft nur
durch Testen aller potentieller Divisoren mittels Polynomdivision entscheiden.
heißt irreduzibel, falls es sich nicht
als Produkt zweier Polynome von echt kleinerem Grad schreiben läßt. Das läßt sich in der Praxis oft nur
durch Testen aller potentieller Divisoren mittels Polynomdivision entscheiden.
So ist zum Beispiel
![]() irreduzibel. Wäre es reduzibel, so hätte es einen Linearfaktor der
Form
irreduzibel. Wäre es reduzibel, so hätte es einen Linearfaktor der
Form
![]() als Teiler, und somit
als Teiler, und somit
![]() als Nullstelle. Das Polynom
als Nullstelle. Das Polynom
![]() hat aber keine Nullstelle in
hat aber keine Nullstelle in
![]() .
.
Dahingegen ist
![]() reduzibel, und zwar als
reduzibel, und zwar als
![]() .
.
Ist
![]() irreduzibel, so bildet
irreduzibel, so bildet
![]() einen Körper.
Die Bezeichnung als
einen Körper.
Die Bezeichnung als
![]() rechtfertigt sich dadurch, daß man zeigen kann, daß dieser Körper im wesentlichen
nur vom Grad
rechtfertigt sich dadurch, daß man zeigen kann, daß dieser Körper im wesentlichen
nur vom Grad
![]() des irreduziblen Polynoms abhängt. Umgekehrt kann man zeigen, daß für alle Primzahlen
des irreduziblen Polynoms abhängt. Umgekehrt kann man zeigen, daß für alle Primzahlen
![]() und für alle
und für alle
![]() wenigstens ein irreduzibles Polynom von Grad
wenigstens ein irreduzibles Polynom von Grad
![]() in
in
![]() existiert (im allgemeinen
sogar recht viele). Kurz,
existiert (im allgemeinen
sogar recht viele). Kurz,
Es ist
![]() , indem Konstanten mit Polynomen von Grad
, indem Konstanten mit Polynomen von Grad
![]() identifiziert werden. So wird
identifiziert werden. So wird
![]() auch ein Vektorraum über
auch ein Vektorraum über
![]() , mit Basis
, mit Basis
![]() . In der Tat ergibt sich mit
Polynomdivision durch
. In der Tat ergibt sich mit
Polynomdivision durch
![]() allgemein in
allgemein in
![]()
Beachte, daß sich der Restklassenring
![]() , der ebenfalls
, der ebenfalls
![]() Elemente enthält, im Falle
Elemente enthält, im Falle
![]() wesentlich
von
wesentlich
von
![]() unterscheidet. Zum Beispiel gilt für
unterscheidet. Zum Beispiel gilt für
![]() stets
stets
 . Dies ist zum Beispiel für
. Dies ist zum Beispiel für
![]() falsch falls
falsch falls
![]() .
.
Primitive Elemente, Zech-Logarithmen
Jedes Element
![]() in
in
![]() erfüllt
erfüllt
![]() .
Ist
.
Ist
![]() der minimale Exponent
der minimale Exponent
![]() , der
, der
![]() zu
zu
![]() macht, so heißt
macht, so heißt
![]() primitiv. Man kann zeigen, daß jeder Körper der Form
primitiv. Man kann zeigen, daß jeder Körper der Form
![]() wenigstens ein primitives Element
enthält. (Ein zufällig ausgewähltes Element wird mit guter Wahrscheinlichkeit primitiv sein.)
wenigstens ein primitives Element
enthält. (Ein zufällig ausgewähltes Element wird mit guter Wahrscheinlichkeit primitiv sein.)
Bezüglich eines fest gewählten primitiven Elements
![]() werden die Zech-Logarithmen wie folgt
definiert. Ist
werden die Zech-Logarithmen wie folgt
definiert. Ist
![]() , so heißt
, so heißt
![]() der Zech-Logarithmus von
der Zech-Logarithmus von
![]() .
Dies legt
.
Dies legt
![]() eindeutig fest, es sei denn, es war
eindeutig fest, es sei denn, es war
![]() . Diesenfalls setzen wir
. Diesenfalls setzen wir
![]() .
.
Für die Addition sind diese Zech-Logarithmen hilfreich, da für
![]()
Betrachten wir einmal den Körper
![]() . Als primitives Element kommt etwa
. Als primitives Element kommt etwa
![]() in Frage. In der Tat
in Frage. In der Tat
![]() ,
,
![]() und
und
![]() .
Die diesbezüglichen Zech-Logarithmen können der Tabelle
.
Die diesbezüglichen Zech-Logarithmen können der Tabelle
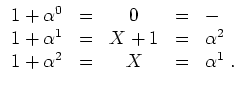
Frobenius
Der Frobenius-Automorphismus von
![]() ist eine bijektive Selbstabbildung von
ist eine bijektive Selbstabbildung von
![]() , gegeben durch
, gegeben durch
![]() . Es gilt
. Es gilt
![]() für
für
![]() , insbesondere also
, insbesondere also
![]() falls
falls
![]() .
Ferner ist
.
Ferner ist
![]() . Iteriertes Anwenden liefert
. Iteriertes Anwenden liefert
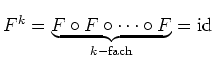 .
.
Beispiele:
| automatisch erstellt am 25. 1. 2006 |