Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Quasilineare partielle Differentialgleichungen erster Ordnung

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Sei $ \mbox{$x = (x_1,\dots, x_n)$}$. Eine partielle Differentialgleichung erster Ordnung der Form

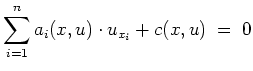
$ \mbox{$\displaystyle \sum_{i = 1}^n a_i(x,u)\cdot u_{x_i} + c(x,u)\; =\; 0 $}$
heißt quasilinear.

Eine solche quasilineare Gleichung wird auf eine lineare Gleichung zurückgeführt, indem die abhängige Variable zu einer zusätzlichen unabhängigen Variablen gemacht wird.

Wir geben uns hier mit einer impliziten Lösung $ \mbox{$f(x,u(x)) = {\mbox{const.}}$}$ zufrieden. Sei also $ \mbox{$f(x,v)$}$ als Funktion angesetzt, die nach Einsetzen einer Lösung $ \mbox{$v = u(x)$}$ konstant in $ \mbox{$x$}$ wird. Die Ableitung nach $ \mbox{$x_i$}$ gibt dann notwendigerweise

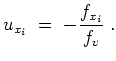
$ \mbox{$\displaystyle u_{x_i}\; =\; -\frac{f_{x_i}}{f_v}\; . $}$
Umgekehrt, ist diese Gleichung für alle $ \mbox{$x_i$}$ erfüllt, so ist $ \mbox{$f(x,u(x))$}$ konstant in $ \mbox{$x$}$. Und dies wollen wir als implizite Lösung unserer quasilinearen Gleichung gelten lassen.

Einsetzen in die Ausgangsgleichung liefert

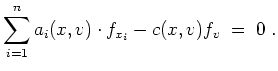
$ \mbox{$\displaystyle \sum_{i = 1}^n a_i(x,v)\cdot f_{x_i} - c(x,v) f_v\; =\; 0\; . $}$
Dies ist eine lineare Rumpfgleichung erster Ordnung für $ \mbox{$f(x,v)$}$, wie oben bereits behandelt. Die allgemeine Lösung ist von der Gestalt
$ \mbox{$\displaystyle f(x,v) = g(\xi(x,v))\; , $}$
wobei $ \mbox{$\xi(x,v) = (\xi_1(x,v),\dots,\xi_n(x,v))$}$ ein unabhängiges System von Partikulärlösungen darstellt, und $ \mbox{$g$}$ eine beliebige Funktion ist - wobei allerdings darauf zu achten ist, daß $ \mbox{$f_v$}$ nicht identisch verschwindet, vgl. Herleitung. Unabhängigkeit ist hier im Sinne einer nicht identisch verschwindenden Jacobideterminante zu verstehen.
(Autoren: Künzer/Meister/Nebe)

Beispiel:

[Verweise]
  automatisch erstellt am 25.  1. 2006