
Mathematik-Online-Lexikon:

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |
|
Mathematik-Online-Lexikon: | |
Lineare partielle Differentialgleichungen zweiter Ordnung (in zwei Variablen) |
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z | Übersicht |
Eine partielle Differentialgleichung zweiter Ordnung in den Variablen
![]() und
und
![]() ist gegeben durch
ist gegeben durch
Die Diskrimante dieser Gleichung ist definiert als
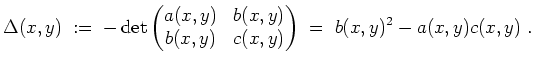
Zunächst wollen wir den Anteil zweiter Ordnung
![]() dieser Gleichung durch eine Transformation
dieser Gleichung durch eine Transformation
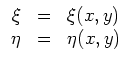
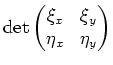 nicht identisch verschwinden darf, damit
wir eine Umkehrtransformation
nicht identisch verschwinden darf, damit
wir eine Umkehrtransformation
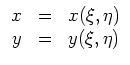
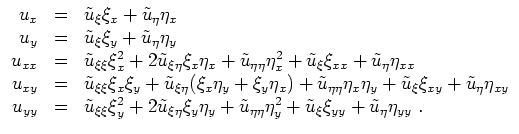
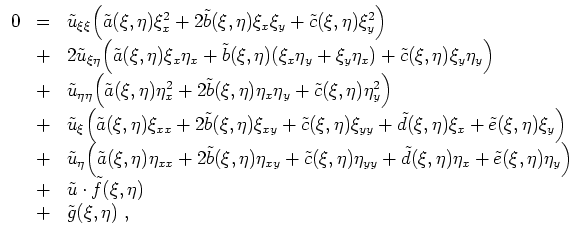
In Differentialoperatoren gesprochen, ist der Anteil zweiter Ordnung gegeben durch
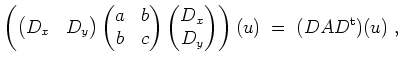
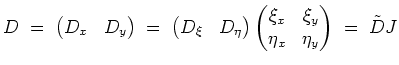
Das Vorzeichen der Diskriminante bleibt wegen
Man wählt die Transformation so, daß die Gleichung in den neuen Variablen eine partielle Differentialgleichung erster Ordnung wird. Naheliegend ist, durch einen Ansatz
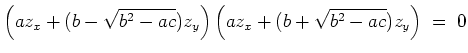
Man unterscheidet im folgenden die Fälle
![]() ,
,
![]() und
und
![]() jeweils auf dem zu untersuchenden Gebiet. Die Fälle, in denen
jeweils auf dem zu untersuchenden Gebiet. Die Fälle, in denen
![]() dort das Vorzeichen
ändert oder nicht identisch verschwindet, werden nicht behandelt.
dort das Vorzeichen
ändert oder nicht identisch verschwindet, werden nicht behandelt.
Für
![]() heißt die Gleichung parabolisch. In diesem Fall ist für die charakteristische Gleichung
die Differentialgleichung
heißt die Gleichung parabolisch. In diesem Fall ist für die charakteristische Gleichung
die Differentialgleichung
Für
![]() heißt die Gleichung hyperbolisch. In diesem Fall bestimme man eine Lösung
heißt die Gleichung hyperbolisch. In diesem Fall bestimme man eine Lösung
![]() des ersten Faktors der charakteristischen Gleichung, und eine
Lösung
des ersten Faktors der charakteristischen Gleichung, und eine
Lösung
![]() des zweiten, unter Beachtung dessen, daß
des zweiten, unter Beachtung dessen, daß
![]() nicht identisch verschwinde.
Damit sind die Koeffizienten von
nicht identisch verschwinde.
Damit sind die Koeffizienten von
![]() und
und
![]() konstant null. Nach Division durch den nicht identisch verschwindenden Koeffizienten von
konstant null. Nach Division durch den nicht identisch verschwindenden Koeffizienten von
![]() bleibt eine Gleichung der Form
bleibt eine Gleichung der Form
Für
![]() heißt die Gleichung elliptisch. In diesem Fall bestimme man für
die charakteristische Gleichung eine komplexe nicht konstante Lösung
heißt die Gleichung elliptisch. In diesem Fall bestimme man für
die charakteristische Gleichung eine komplexe nicht konstante Lösung
![]() von
von
![]() .
Substituiert man
.
Substituiert man
![]() und
und
![]() , so verschwindet der Realteil der charakteristischen Gleichung; es ist also
, so verschwindet der Realteil der charakteristischen Gleichung; es ist also
Beispiele:
| automatisch erstellt am 25. 1. 2006 |