Mathematik-Online-Lexikon: Rationale Zahlen

	[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
	Mathematik-Online-Lexikon:
	Rationale Zahlen

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Übersicht

Die rationalen Zahlen bestehen aus positiven und negativen Brüchen:

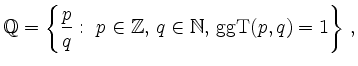
$\displaystyle {\mathbb{Q}} = \left\{\frac{p}{q}:\ p\in{\mathbb{Z}},\, q\in\mathbb{N},\, \operatorname{ggT}(p,q)=1 \right\} \,,$

mit $\operatorname{ggT}$ dem größten gemeinsamen Teiler. Sie bilden bzgl. Addition und Multipliktion einen Körper.

$\includegraphics[width=.35\linewidth]{cantor.epsf}$

Die Menge $\mathbb{Q}$ ist abzählbar. Wie in der Abbildung illustriert ist, können die positiven Brüche mit dem sogenannten Diagonalverfahren in einer Folge angeordnet werden. Dabei werden die kürzbaren Brüche beim Abzählen übersprungen.

Schließlich bilden die rationalen Zahlen eine dichte Teilmenge der Zahlengraden. Zwischen zwei verschiedenen rationalen Zahlen liegen unendlich viele rationale Zahlen.

siehe auch:

Stichwort: Zahlen: rationale

automatisch erstellt am 19. 8. 2013