Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] Englische Flagge
Mathematik-Online-Lexikon:

Transformation des Integrationsbereiches

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht
Für eine bijektive, stetig differenzierbare Transformation $ g$ eines regulären Bereiches $ U \subseteq \mathbb{R}^n$ mit

$\displaystyle \operatorname{det}g^\prime(x)\ne 0,\quad x\in U \,, $

gilt für stetige Funktionen $ f$:

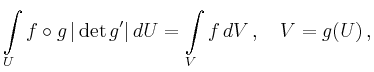
$\displaystyle \int\limits_U f\circ g\, \vert\operatorname{det}g^\prime\vert\,dU = \int\limits_V f\,dV\,,\quad V=g(U)\,, $

wobei $ \operatorname{det} g'$ als Funktionaldeterminante der Transformation bezeichnet wird. Sie beschreibt die lokale Änderung des Volumenelementes

$\displaystyle d V = \vert\operatorname{det} g^\prime\vert \, dU \,. $

\includegraphics[width=\moimagesize]{a_trans_mehr_3}

Für eine lokal orthogonale Koordinatentransformation $ g$, d. h. bei orthogonalen Spalten von $ g^\prime$, ist

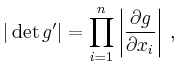
$\displaystyle \vert\operatorname{det}g^\prime\vert = \prod_{i=1}^n \left\vert \frac{\partial g}{\partial x_i} \right\vert \,, $

d.h., der Skalierungsfaktor des Volumenelements ist das Produkt der Skalierungsfaktoren der einzelnen Variablen.

Bei einer affinen Transformation $ y=Ax+b$ ändert sich das Volumenelement gemäß

$\displaystyle dy = \vert\operatorname{det}A\vert\,dx \,. $

Insbesondere gilt für eine Skalierung der Variablen, $ y_i=\lambda_i x_i$

$\displaystyle dy_i = \lambda_i\,dx_i \,. $

Die Voraussetzungen können etwas abgeschwächt werden. Insbesondere muss die Bijektivität von $ g$ und die Invertierbarkeit von $ g^\prime$ nur im Innern von $ U$ gefordert werden. Unstetigkeiten von $ f$ und bestimmte Singularitäten sind ebenfalls möglich, wenn die Existenz beider Integrale gewährleistet ist.

siehe auch:

[Erläuterungen] [Beispiele]
  automatisch erstellt am 19.  8. 2013