
Mathematik-Online-Lexikon:

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |
|
Mathematik-Online-Lexikon: | |
Laplace-Transformation einer linearen Differentialgleichung zweiter Ordnung |
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z | Übersicht |
Die Laplace-Transformation der Lösung des Anfangswertproblems
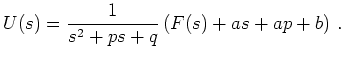
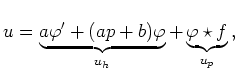
Bezeichnen ![]() und
und ![]() die Nullstellen des charakteristischen Polynoms
die Nullstellen des charakteristischen Polynoms
![]() , so gilt
, so gilt
![$\displaystyle \varphi(t) = \left\{\begin{array}{cr} \displaystyle{ \frac{e^{\la...
...\\ [-1ex]
\\
t e^{\lambda t}\,,\quad &\lambda = \varrho\,. \end{array}\right.
$](/inhalt/aussage/aussage747/img8.png)
siehe auch:
| automatisch erstellt am 19. 8. 2013 |