Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] Englische Flagge
Mathematik-Online-Lexikon:

Reelle Fourier-Reihe

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht
Die reelle Fourier-Reihe einer reellen $ 2\pi$-periodischen Funktion $ f$ ist die Entwicklung nach dem Orthogonalsystem der Kosinus- und Sinusfunktionen:

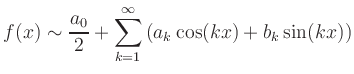
$\displaystyle f(x) \sim \frac{a_0}{2} + \sum_{k=1}^\infty \left( a_k\cos(kx)+b_k\sin(kx)\right) $

mit

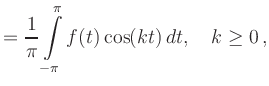$\displaystyle a_k$ $\displaystyle = \frac{1}{\pi} \int\limits_{-\pi}^\pi f(t)\cos(kt)\,dt,\quad k\ge0\,,$    
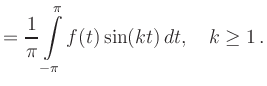$\displaystyle b_k$ $\displaystyle = \frac{1}{\pi} \int\limits_{-\pi}^\pi f(t)\sin(kt)\,dt,\quad k\ge1\,.$    

Die Art der Konvergenz der Reihe hängt dabei von der Glattheit von $ f$ ab. Hinreichend für absolute Konvergenz ist beispielsweise, dass die Fourier-Koeffizienten $ a_k$ und $ b_k$ absolut konvergente Reihen bilden.

Auch eine konvergente Fourier-Reihe muss nicht an allen Stellen den Funktionswert als Grenzwert haben. An Unstetigkeitsstellen konvergiert die Reihe meist gegen den Mittelwert aus rechtsseitigem und linksseitigem Funktionsgrenzwert. Daher wird im Allgemeinen $ f(x) \sim \sum \cdots$ statt $ f(x)= \sum \cdots$ geschrieben.

Beispiel:

[Verweise]
  automatisch erstellt am 22.  9. 2016