Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] Englische Flagge
Mathematik-Online-Lexikon:

Ordnungsrelation reeller Zahlen

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Auf der Zahlengeraden können reelle Zahlen verglichen werden. Man definiert für $ a,b,c \in {\mathbb{R}}$

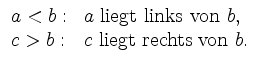
$\displaystyle \begin{array}{ll} a < b: & \mbox{$a$\ liegt links von $b$,} \\ c > b: & \mbox{$c$\ liegt rechts von $b$.} \end{array}$

Ist bei dem Vergleich die Gleichheit zugelassen, so verwendet man die Symbole $ \le$ und $ \ge$.

\includegraphics[width=.5\linewidth]{a_ordnung_reeller_zahlen}

Die positiven rellen Zahlen bezeichnet man mit

$\displaystyle \mathbb{R}^+ = \{x\in\mathbb{R}:\ x>0\} $

und die negaitven mit $ \mathbb{R}^-$. Darüber hinaus schreibt man $ \mathbb{R}_0^+ = \mathbb{R}^+\cup\{0\}$.

Die reellen Zahlen sind bzgl. der Ordnungsrelation vollständig, d.h. für jede beschränkte Menge reller Zahlen existiert eine kleinste obere (Supremum) und größte untere Schranke (Infimum) in $ \mathbb{R}$.

siehe auch:

  automatisch erstellt am 19.  8. 2013