Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] Englische Flagge
Mathematik-Online-Lexikon:

4-Punkt Schema

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Zur genauen grafischen Darstellung von Funktionen aus Werten $ f_k$ an äquidistanten Stützstellen $ x_k=kh$ kann kubische Interpolation verwendet werden. Dabei werden Zwischenwerte an den Stützstellen $ x_{k+1/2}=(k+1/2)h$ durch

$\displaystyle f_{k+1/2} = (-f_{k-1}+9f_k+9f_{k+1}-f_{k+2})/16 $

approximiert. Dieser Prozess wird wiederholt, bis genügend Daten generiert wurden.

Die Gewichte

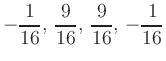
$\displaystyle -\frac{1}{16},\, \frac{9}{16},\, \frac{9}{16},\, -\frac{1}{16} $

der $ 4$-Punkt-Formel sind die Werte der Lagrange-Polynome an der Stützstelle $ x_{k+1/2}$. Beispielsweise ist

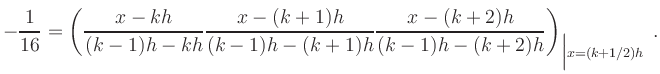
$\displaystyle -\frac{1}{16} = \left( \frac{x-kh}{(k-1)h-kh} \frac{x-(k+1)h}... ...+1)h} \frac{x-(k+2)h}{(k-1)h-(k+2)h} \right)_{\Big\vert x = (k+1/2)h} \,. $

Aufgrund der Symmetrie und da die Koeffizienten zu eins summieren (Interpolation konstanter Daten), ergeben sich die anderen Koeffizienten ohne Rechnung.

\includegraphics[width=.45\textwidth]{KubischeInterpolation_Bild1} \includegraphics[width=.45\textwidth]{KubischeInterpolation_Bild2}
\includegraphics[width=.45\textwidth]{KubischeInterpolation_Bild3} \includegraphics[width=.45\textwidth]{KubischeInterpolation_Bild4}

Die Abbildung zeigt die Ausgangsdaten und durch dreimalige Anwendung der $ 4$-Punkt-Interpolation erzeugte Approximationen einer Sinusfunktion. Zwar wirkt die unten links gezeigte Grenzfunktion glatt. Jedoch ist nur die erste Ableitung stetig.

\includegraphics[width=.4\textwidth]{fourpoint_lim}          \includegraphics[width=.4\textwidth]{fourpoint_diff}

Die rechte Grafik zeigt die durch Dividierte Differenzen angenäherte zweite Ableitung nach achtmaliger Interpolation. Man erkennt den fraktalen Charakter des Graphen.

[Verweise]
  automatisch erstellt am 22.  6. 2016