Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Beispiel: Ableitung der Umkehrfunktion

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht
Die Funktion

$\displaystyle y = f(x) = x\,(1-x) $

besitzt auf den Intervallen $ (-\infty,1/2]$ und $ [1/2, \infty)$ jeweils eine Umkehrfunktion $ x = g(y)$ .
\includegraphics[width=0.5\linewidth]{a_umkehrfunktion_1.eps}
In beiden Fällen gilt

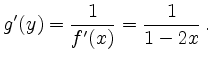
$\displaystyle g'(y) = \frac{1}{f'(x)} = \frac{1}{1-2x}\,. $

Nochmaliges Differenzieren ergibt

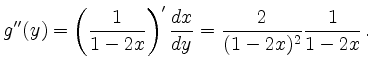
$\displaystyle g''(y) = \left( \frac{1}{1-2x}\right)' \frac{dx}{dy} = \frac{2}{(1-2x)^2} \frac{1}{1-2x}\,. $

Speziell erhält man für $ x = 1, y = 0$

$\displaystyle g'(0) = 1 ,\quad g''(0) = -2\,. $

Die Ableitungen sind also berechenbar, ohne dass die Umkehrfunktion explizit gebildet werden muss. Dies ist nur dann möglich, wenn man $ g'(y)$ als Funktion von $ y$ schreiben kann. In diesem Beispiel ist das möglich, denn $ x$ lässt sich als Funktion von $ y$ schreiben:

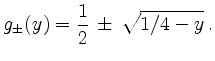
$\displaystyle g_{\pm}(y) = \frac{1}{2}\,\pm\,\sqrt{1/4 - y}\,. $

Die obigen Werte können so überprüft werden, wobei der dem Wertepaar $ (1, 0)$ entsprechende Zweig gewählt werden muss.

(Autoren: Höllig/Kreitz )

siehe auch:

  automatisch erstellt am 17.  4. 2008