
Mathematik-Online-Lexikon:

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |
|
Mathematik-Online-Lexikon: | |
Abstandsbestimmung |
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z | Übersicht |
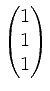 von der Ebene
von der Ebene
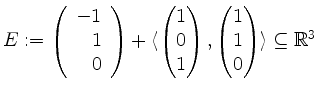 .
.
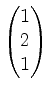 von der Geraden
von der Geraden
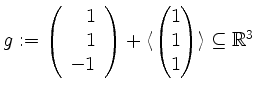 .
.
Lösung.
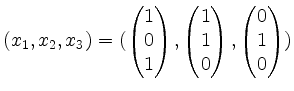 , gibt
, gibt
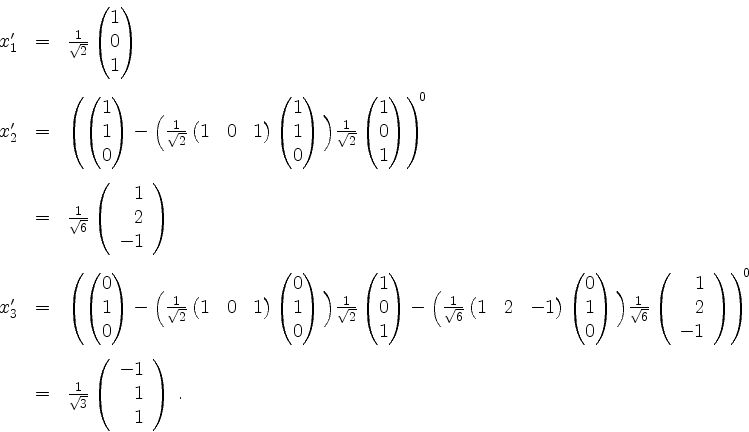
Damit erhalten wir
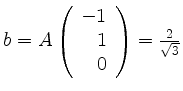
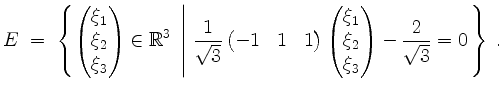
Der Abstand von
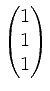 zu
zu
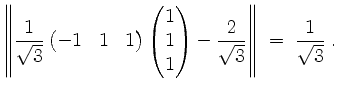
Alternativ erhält man den Vektor
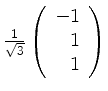 , orthogonal zu den Erzeugern
, orthogonal zu den Erzeugern
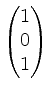 und
und
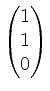 , auch
als normierten Vektor von
, auch
als normierten Vektor von
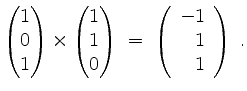
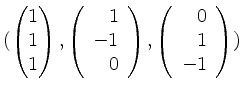 , gibt
, gibt
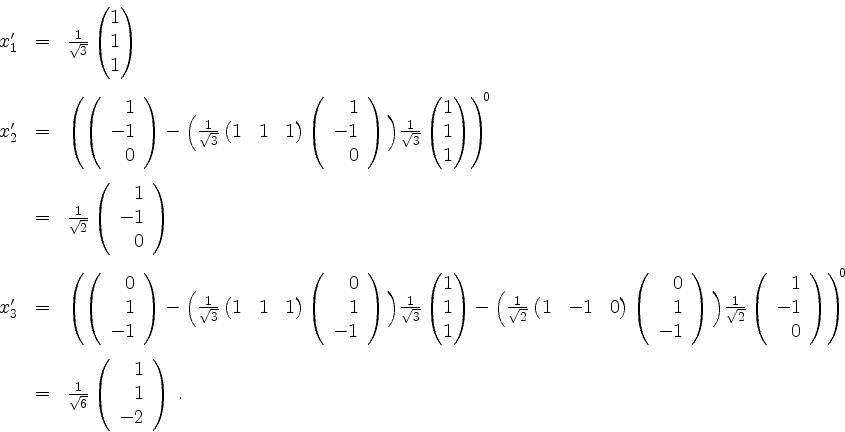
Damit erhalten wir
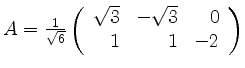 und
und
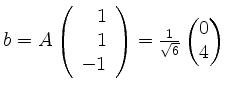 . Es wird
. Es wird
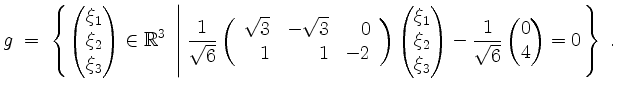
Der Abstand von
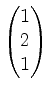 zu
zu
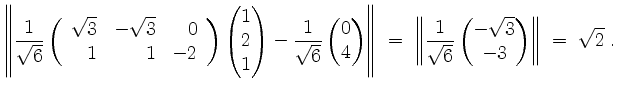
Alternativ, findet man einen Vektor wie
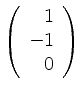 , der orthogonal zu
, der orthogonal zu
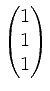 steht, so kann man den dritten Vektor einer Orthormalbasis als
normierten Vektor von
steht, so kann man den dritten Vektor einer Orthormalbasis als
normierten Vektor von
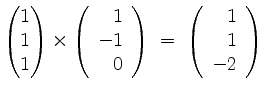
finden.
siehe auch:
| automatisch erstellt am 11. 8. 2006 |