
Mathematik-Online-Lexikon:

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |
|
Mathematik-Online-Lexikon: | |
Volumen eines Kegels |
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z | Übersicht |
![$\displaystyle K=\left\{\left.\lambda\begin{pmatrix}a_1\\ a_2\\ h\end{pmatrix}+(...
...\vert\;
\lambda\in[0,1],\; \begin{pmatrix}x_1\\ x_2\end{pmatrix}\in M\right\}
$](/inhalt/beispiel/beispiel1144/img4.png)
der Kegel im
Lösung.
Für ![]() ergibt sich der
ergibt sich der ![]() -Schnitt von
-Schnitt von ![]() zu
zu
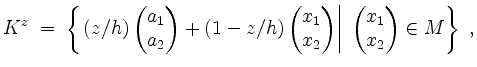
denn in der Darstellung
![$\displaystyle K \;=\;
\left\{\left.\lambda\begin{pmatrix}a_1\\ a_2\\ h\end{pmat...
...\vert\;
\lambda\in[0,1],\; \begin{pmatrix}x_1\\ x_2\end{pmatrix}\in M\right\}
$](/inhalt/beispiel/beispiel1144/img12.png)
sind die Punkte mit dritter Koordinate
Die Menge ![]() entsteht aus
entsteht aus ![]() durch eine Verschiebung und eine Streckung um den Faktor
durch eine Verschiebung und eine Streckung um den Faktor ![]() . Daher gilt
. Daher gilt
Ferner ist
![]() für
für
![]() . Also ist die Projektion von
. Also ist die Projektion von ![]() auf die
auf die ![]() -Achse gegeben durch
-Achse gegeben durch ![]() .
Nach dem Prinzip von Cavalieri folgt
.
Nach dem Prinzip von Cavalieri folgt
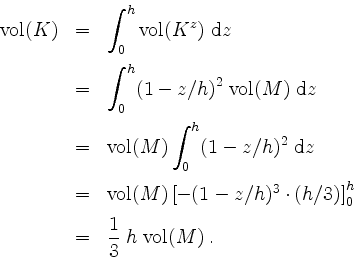
Kurz, das Volumen des Kegels ist gleich
![]()
![]() Höhe
Höhe ![]() Grundfläche.
Grundfläche.
| automatisch erstellt am 11. 8. 2006 |