
Mathematik-Online-Lexikon:

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |
|
Mathematik-Online-Lexikon: | |
Volumen des Parallelepipeds |
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z | Übersicht |
Sei ![]() . Sei
. Sei
![]() ein linear unabhängiges Tupel von Vektoren in
ein linear unabhängiges Tupel von Vektoren in
![]() , und sei
, und sei
![$\displaystyle \mathfrak{P}(p_1,\ldots,p_n):=\left\{ \left. \sum\limits_{i=1}^{n} \lambda_i p_i \right\vert \lambda_1, \ldots, \lambda_n \in [0,1] \right\}
$](/inhalt/beispiel/beispiel1146/img4.png)
das von
Lösung.
Sei
![]() die Matrix, welche als
die Matrix, welche als ![]() -te Spalte
-te Spalte ![]() beinhaltet.
beinhaltet.
Sei
![]() ,
,
![]() . Dann ist
. Dann ist
![]() .
.
Gemäß Substitutionsregel erhalten wir
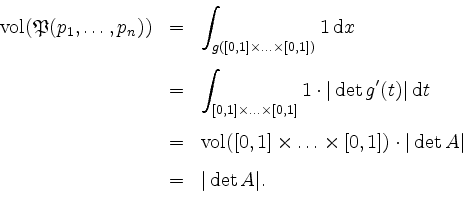
| automatisch erstellt am 11. 8. 2006 |