Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Inhalt und Integral einer Kugelkappe

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Sei $ R > 0$ . Es seien

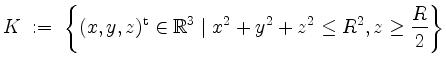
$\displaystyle K \; :=\; \left\{ (x,y,z)^\mathrm{t} \in \mathbb{R}^3 \; \vert\; x^2 + y^2 + z^2 \leq R^2, z \geq \frac{R}{2} \right\} $

und

$\displaystyle f(x,y,z) \; :=\; y^2 z \;. $

Bestimme das Volumen von $ K$ . Berechne $ \displaystyle \int_K f$ .

Lösung.

Wir bestimmen zunächst das Volumen von $ K$ . Geometrisch ist $ K$ eine obere Kuppe einer Kugel. Aufgrund der Bedingung $ z \geq R/2$ ist es an dieser Stelle nicht ratsam, Kugelkoordinaten zu betrachten.

Statt dessen erhalten wir mit dem Satz von Fubini und der Kenntnis, daß ein Kreis mit Radius $ r$ den Inhalt $ \pi r^2$ besitzt, daß

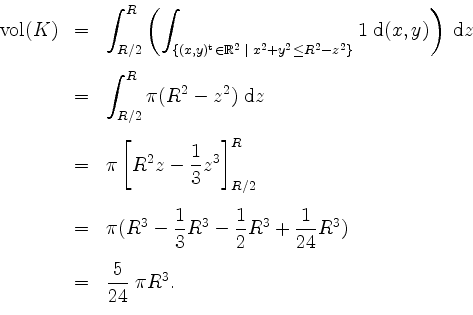
\begin{displaymath} \begin{array}{rcl} \mathrm{vol}(K) & = & \displaystyle \int... ... R^3)\vspace{3mm}\\ & = & \dfrac{5}{24}\;\pi R^3. \end{array}\end{displaymath}

Probe. Dimensionstest. Das Resultat sollte, wenn man Längeneinheiten einführt, von der Dimension $ (\mathrm{L''angeneinheit})^3$ sein, kurz, es sollte dreidimensional sein. Dies ist der Fall. Auch von der Größenordnung ist es etwas kleiner als ein Viertel des Kugelvolumens, nämlich kleiner als $ \pi R^3/3$ . Auch dies stimmt mit der Anschauung überein.

Analog berechnen wir mittels Polarkoordinatentransformation (oder, je nach Interpretation des Geschehens, mit Zylinderkoordinaten)

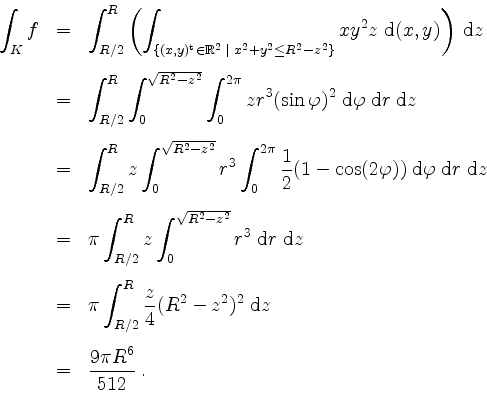
\begin{displaymath} \begin{array}{rcl} \displaystyle\int_K f & = & \displayst... ... & = & \displaystyle \frac{9\pi R^6}{512}\; . \\ \end{array}\end{displaymath}

Probe. Dimensionstest. Die Funktion $ f(x,y,z) = y^2 z$ hatte einen dreidimensionalen Wert (daher funktioniert der Test), und $ K$ ist ein dreidimensionales Gebilde. Das Ergebnis sollte also Dimension $ 3 + 3 = 6$ haben.

(Autoren: Künzer/Martin/Tentler/Wahrheit)

siehe auch:

  automatisch erstellt am 11.  8. 2006