Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Ein Oberflächenintegral

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Es sei das Vektorfeld $ f:\mathbb{R}^3\to\mathbb{R}^3$ , $ f(x,y,z)=(-y,x,xyz)^\mathrm{t}$ , gegeben.

Es bezeichne $ \Phi$ eine Fläche, deren Träger die Oberfläche der oberen Halbkugel vom Radius $ 1$ ist. Die Parametrisierung sei dabei so gewählt, daß der zugehörige Normalenvektor stets nicht nach unten zeige.

Berechne das Oberflächenintegral $ \int_\Phi \mathrm{rot }f$ einmal unter Verwendung des Stokesschen Integralsatzes und einmal durch direkte Rechnung.

Lösung.

Wir berechnen das Oberflächenintegral mit dem Stokesschen Integralsatz. Um die Halbkugel zu parametrisieren, wählen wir die Fläche

$\displaystyle \Phi:\underbrace{[0,\pi/2]\times [-\pi,\pi]}_{=:K} \to\mathbb{R}^... ...\psi)(\cos \varphi)\\ (\sin \psi)(\sin \varphi)\\ \cos \psi \end{pmatrix}\;. $

Den Rand $ \partial K$ von $ K$ , der sich aus vier Geradenstücken zusammensetzt, beschreiben wir durch die folgenden vier ebenen Kurven.

\begin{displaymath} \begin{array}{rcll} \alpha(t) &=& (0,-t)^\mathrm{t}\; , & t\... ...pi)^\mathrm{t}\; , & t\in [-\frac{\pi}{2},0]\;. \\ \end{array}\end{displaymath}

Der Rand $ \partial\Phi=\Phi\circ\partial K$ der Fläche $ \Phi$ wird also beschrieben durch die vier Raumkurven

\begin{displaymath} \begin{array}{rcll} (\Phi\circ\alpha)(t) &=& (0,\; 0,\; 1)^\... ...\cos t)^\mathrm{t}\; , & t\in [-\frac{\pi}{2},0]\;. \end{array}\end{displaymath}

Eine Betrachtung dieser Wege wird die Rechnung erleichtern. Zunächst ist $ \Phi\circ\alpha$ ein konstanter Weg, d.h. ein Kurvenintegral längs dieses Weges ist 0 . Ferner ist $ \Phi\circ\beta$ genau der zu $ \Phi\circ\delta$ entegegengestetzte Weg. Die Kurvenintegrale längs dieser beiden Wege heben sich gegenseitig auf.

Der Stokessche Integralsatz liefert somit

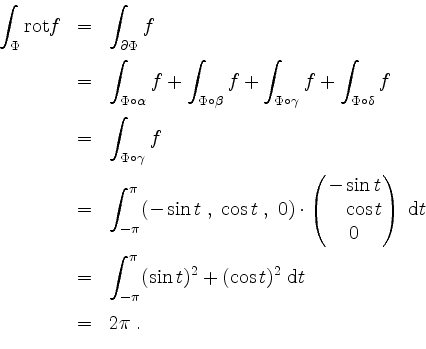
\begin{displaymath} \begin{array}{rcl} \displaystyle\int_\Phi \mathrm{rot }f &=&... ...(\cos t)^2\;\mathrm{d}t\vspace*{2mm}\\ &=& 2\pi\;. \end{array}\end{displaymath}

Wollten wir das gegebene Oberflächenintegral direkt berechnen, bestimmen wir noch

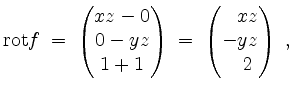
$\displaystyle \mathrm{rot }f \;=\; \begin{pmatrix}xz-0\\ 0-yz\\ 1+1\end{pmatrix}\;=\; \begin{pmatrix}\phantom{-}xz\\ -yz\\ \phantom{-}2\end{pmatrix}\;, $

sowie

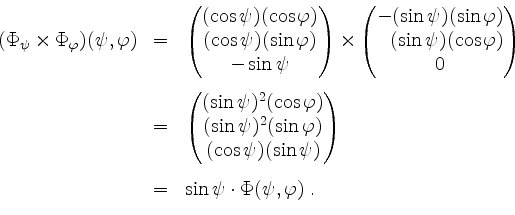
\begin{displaymath} \begin{array}{rcl} (\Phi_\psi \times \Phi_\varphi)(\psi,\var... ...pace{3mm}\\ &=& \sin\psi\cdot\Phi(\psi,\varphi)\;. \end{array}\end{displaymath}

Damit ist auch geklärt, daß der Normalenvektor nichtnegative dritte Koordinate hat, d.h. nicht nach unten zeigt. Nach Definition des Oberflächenintegrals ist dann

\begin{displaymath} \begin{array}{rcl} \displaystyle\int_\Phi \mathrm{rot }f &=&... ...psi)^2\right]_0^{\pi/2}\vspace*{2mm}\\ &=& 2\pi\;. \end{array}\end{displaymath}

Für das drittletze Gleichheitszeichen beachte man $ \int_{-\pi}^\pi\cos(2\varphi)\;\mathrm{d}\varphi=0$ .
(Autoren: Künzer/Martin/Tentler/Wahrheit)

siehe auch:

  automatisch erstellt am 11.  8. 2006