
Mathematik-Online-Lexikon:

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |
|
Mathematik-Online-Lexikon: | |
Ein System linearer Differentialgleichungen |
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z | Übersicht |
Löse das System
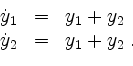
Lösung.
Wir haben
![]() zu lösen, wobei
zu lösen, wobei
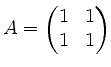 .
.
Nun ist
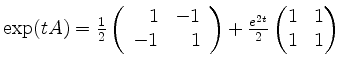 eine Fundamentalmatrix.
eine Fundamentalmatrix.
Dies kann man
![]() , wobei
, wobei ![]() , und der Reihendarstellung von
, und der Reihendarstellung von ![]() oder aber einer Jordanformüberlegung entnehmen.
oder aber einer Jordanformüberlegung entnehmen.
Eine beliebige Lösung des gegebenen Systems von Differentialgleichungen ist also von der Form
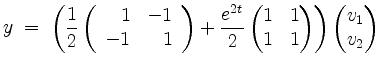
für
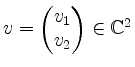 beliebig. Ausgeschrieben bedeutet dies
beliebig. Ausgeschrieben bedeutet dies
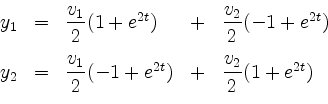
für beliebige
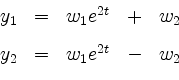
für beliebige
| automatisch erstellt am 11. 8. 2006 |