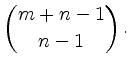Auf wie viele verschiedene Arten lässt sich die Zahl 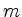 als Summe von
als Summe von 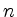 -Zahlen
-Zahlen
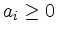 schreiben,
wobei die Reihenfolge zu beachten ist? Es wird also die Anzahl der
schreiben,
wobei die Reihenfolge zu beachten ist? Es wird also die Anzahl der
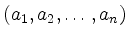 mit
mit
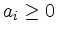 und
gesucht.
und
gesucht.
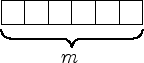
Um die Frage zu lösen stellt man sich die Zahl 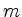 als eine Folge von
als eine Folge von 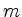 Kästchen vor:
Kästchen vor:
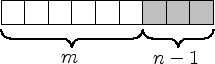
An diese 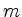 Kästchen werden nun
Kästchen werden nun 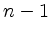 Kästchen angehängt:
Von diesen
Kästchen angehängt:
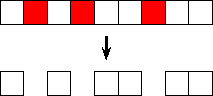
Von diesen 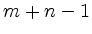 Kästchen werden nun
Kästchen werden nun 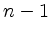 beliebige Kästchen entfernt, z.B.
beliebige Kästchen entfernt, z.B.
Das Ergebnis sind insgesamt 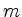 Kästchen die in
Kästchen die in 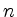 Blöcke zerlegt sind. Die vorangegangen Bilder sind ein
Beispiel für die Zerlegung von
Blöcke zerlegt sind. Die vorangegangen Bilder sind ein
Beispiel für die Zerlegung von 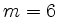 in
in 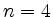 Zahlen und entspricht der Zerlegung
Zahlen und entspricht der Zerlegung
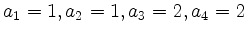 also
also 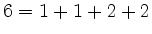 .
.
Es sind noch die folgenden Sonderfälle zu beachten:
- Werden
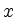 nebeneinander liegende Kästchen entfernt, dann entspricht das an entsprechender Stelle
nebeneinander liegende Kästchen entfernt, dann entspricht das an entsprechender Stelle 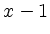 Blöcken der Länge Null und es müssen in der Zerlegung
Blöcken der Länge Null und es müssen in der Zerlegung 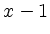 Nullen eingefügt. Es sind also z.B. für
Nullen eingefügt. Es sind also z.B. für 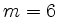 und
und
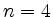 Zerlegungen in
Zerlegungen in 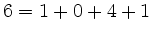 und
und 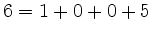 .
.
- Werden die ersten oder die letzte
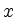 -Kästchen entfernt, dann beginnt, bzw. endet die Zerlegung mit
-Kästchen entfernt, dann beginnt, bzw. endet die Zerlegung mit 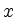 Nullen,
z.B.
entspricht
Nullen,
z.B.
entspricht 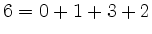 und
und 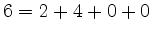 .
.
Man sieht, dass unterschiedliche Arten die Kästchen zu entfernen auch unterschiedliche Zerlegungen liefern.
Außerdem lässt sich jede Zerlegung von 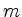 in dieser Art darstellen. Es gibt also genau so viele Zerlegungen
der Zahl
in dieser Art darstellen. Es gibt also genau so viele Zerlegungen
der Zahl 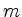 in eine Summe von
in eine Summe von 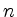 Zahlen
Zahlen
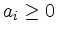 , wie es Möglichkeiten gibt aus einer
, wie es Möglichkeiten gibt aus einer
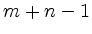 -elementigen Menge eine
-elementigen Menge eine 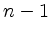 -elementige Teilmenge zu wählen, also ist die Anzahl
-elementige Teilmenge zu wählen, also ist die Anzahl
(Aus: Vorkurs Mathematik)
siehe auch:
| |
automatisch erstellt
am 26. 2. 2007 |


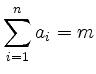
![]() als eine Folge von
als eine Folge von ![]() Kästchen vor:
Kästchen vor:
![]() Kästchen die in
Kästchen die in ![]() Blöcke zerlegt sind. Die vorangegangen Bilder sind ein
Beispiel für die Zerlegung von
Blöcke zerlegt sind. Die vorangegangen Bilder sind ein
Beispiel für die Zerlegung von ![]() in
in ![]() Zahlen und entspricht der Zerlegung
Zahlen und entspricht der Zerlegung
![]() also
also ![]() .
.