Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] Englische Flagge
Mathematik-Online-Lexikon:

Arbeit im Gravitationsfeld

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Ein Planet der Masse $ M$ erzeugt ein Gravitationsfeld, bei dem auf einen Körper der Masse $ m$ die Kraft $ F(x) = \gamma \frac{mM}{x^2}$ ausgeübt wird. Dabei ist $ \gamma$ die Gravitationskonstante und $ x$ der Abstand der Schwerpunkte.

Eine Stammfunktion für $ 1/x^2$ ist $ -1/x$. Um einen Körper vom Abstand $ a$ zum Abstand $ b$ zu bringen, muss somit die Arbeit

$\displaystyle \int_a^b F(x)\,dx = \gamma mM \int_a^b \frac{1}{x^2}\,dx= -\left[ \gamma mM/x \right]_a^b = \gamma mM(1/a-1/b) $

verrichtet werden.

Für $ a$ gleich dem Radius des Planeten und $ b \to \infty$ lässt sich durch Gleichsetzen mit der kinetischen Energie die sogenannte Fluchtgeschwindigkeit $ v$ bestimmen, d.h. die Geschwindigkeit, die notwendig ist, um das Gravitationsfeld eines Planeten zu verlassen:

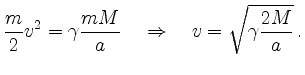
$\displaystyle \frac{m}{2}v^2 = \gamma \frac{mM}{a} \quad \Rightarrow \quad v = \sqrt{\gamma \frac{2M}{a}}\,. $

Am Äquator ist für die Erde $ v = 11.2$km/s.
(Autoren: Höllig/Hörner)

siehe auch:

  automatisch erstellt am 8.  4. 2008