Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Beispiel: Reelle Ungleichung

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht
Die Ungleichung

$\displaystyle -x^2 > x-2 \ , \ {D}=\mathbb{R} $

kann z.B. folgendermaßen umgeformt werden:

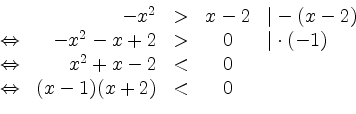
\begin{displaymath} \begin{array}{crccl} &-x^2 & > & x-2 &\vert-(x-2)\\ \Leftri... ...^2+x-2 &< &0 \\ \Leftrightarrow & (x-1)(x+2) &< &0 \end{array}\end{displaymath}

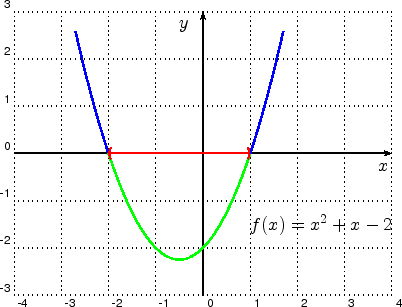
Graphisch kann man die Lösungsmenge als die $ x$-Werte bestimmen, für die das Schaubild der Funktion $ f(x)=x^2+x-2$ echt unter $ x$-Achse verläuft. Im folgenden Bild ist dieser Bereich grün gekennzeichnet, die Lösungsmenge ist das rot eingezeichnete Intervall $ (-2,1)$ der $ x$-Achse (die Grenzen $ x=-2$ und $ x=1$ sind keine Elemente der Lösungsmenge).

\includegraphics{bild04}

Zur rechnerischen Lösung bestimmt man zunächst die Nullstellen der linken Seite. Diese können aus der letzten der obigen Ungleichungen direkt als $ x_1=-2$ und $ x_2=1$ abgelesen werden. Durch Einsetzten von $ x=0$ in die Ungleichung erkennt man, dass $ x=0$ Element der Lösungsmenge ist. Es gilt also $ x^2+x-2 \leq 0$ für $ -2 \leq x \leq 1$ und damit ist $ {L}=\{x\in \mathbb{R} \ : \ -2 < x < 1\}$ die Lösungsmenge der Ungleichung.

(Autor: Vorkurs Mathematik)

siehe auch:

  automatisch erstellt am 23. 10. 2007