Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Beispiel: Lineare Betragsungleichung

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht
Beim Lösen von Betrags(un)gleichungen sind in der Regel Fallunterscheidungen notwendig. Dabei müssen die Fälle, dass das Argument größer oder gleich Null, bzw. kleiner Null ist separat betrachtet werden. Die Betragsungleichung

$\displaystyle -\vert x\vert \leq x-2 \ ; \ x \in \mathbb{R} $

kann rechnerisch folgendermaßen gelöst werden:

Fall 1: Ist $ x \geq 0$ dann lautet die Ungleichung

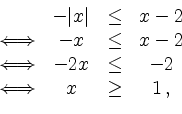
\begin{displaymath} \begin{array}{cccc} &-\vert x\vert &\leq &x-2\\ \Longleftri... ...\leq & -2\\ \Longleftrightarrow & x & \geq & 1 \,, \end{array}\end{displaymath}

d.h. im ersten Fall ($ x \geq 0$) ergibt sich also $ {L}_1=\{x \in \mathbb{R} \ : \ x \geq 1\}$ als Lösungsmenge.

Fall 2: Ist $ x <0 $ dann lautet die Ungleichung

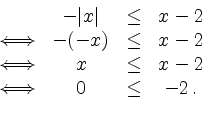
\begin{displaymath} \begin{array}{cccc} &-\vert x\vert &\leq &x-2\\ \Longleftri... ...eq &x- 2\\ \Longleftrightarrow & 0 & \leq & -2 \,. \end{array}\end{displaymath}

Die letzte Ungleichung ist immer falsch. Im zweiten Fall ($ x <0 $) gibt es also keine Lösung, d.h. $ {L}_2=\emptyset$.

Insgesamt erhält man also als Lösungsmenge für die Ungleichung

$\displaystyle {L} =\mathcal{L}_1=\{x \in \mathbb{R} \ : \ x \geq 1\}=[1,\infty)\,.$

Diese Lösung kann auch graphisch bestimmt werden. Setzt man die linke Seite $ f(x)=-\vert x\vert$ und die rechte Seite $ g(x)=x-2$, dann erhält man die Schaubilder

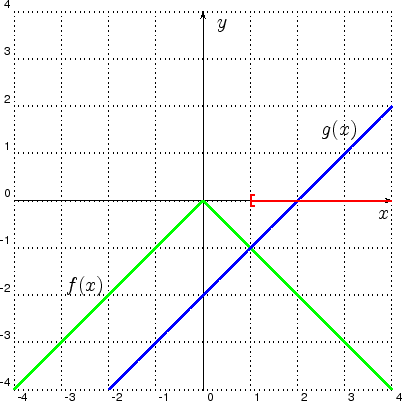
\includegraphics{bild06}

Das rot eingezeichnete Intervall $ [1,\infty)$ ist der Bereich in dem die (grüne) linke Seite $ f(x)=-\vert x\vert$ kleiner oder gleich der (blauen) rechten Seite $ g(x)=x-2$ ist. Das rote Intervall $ [1,\infty)$ beschreibt also die Lösung der Ungleichung $ f(x) \leq g(x)$.

(Autor: Vorkurs Mathematik)

siehe auch:

  automatisch erstellt am 23. 10. 2007